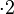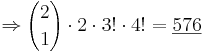2004 IV: Unterschied zwischen den Versionen
K (2. Lösung zu Aufgabe 3b) |
|||
| (3 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 29: | Zeile 29: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
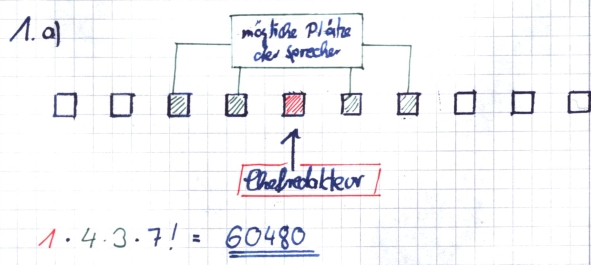
| − | An der Podiumsdiskussion nehmen neben dem Chefredakteur 5 Gegner und 4 Befürworter des Projekts teil. Die 10 Plätze auf dem Podium sind in einer Reihe nebeneinander angeordnet. Der Chefredakteur setzt sich auf den 5. Platz von links. Die beiden | + | An der Podiumsdiskussion nehmen neben dem Chefredakteur 5 Gegner und 4 Befürworter des Projekts teil. Die 10 Plätze auf dem Podium sind in einer Reihe nebeneinander angeordnet. Der Chefredakteur setzt sich auf den 5. Platz von links. Die beiden Gruppen haben jeweils einen Sprecher. |
| Zeile 39: | Zeile 39: | ||
[[Bild:Stochastik04IV1a.jpg|750px]] | [[Bild:Stochastik04IV1a.jpg|750px]] | ||
}} | }} | ||
| + | <popup name="2. Lösung"> | ||
| + | zwei Sprecher auf vier Plätze verteilen, wobei die zwei Sprecher untereinander tauschen können: <math>{4 \choose 2} \cdot 2!</math><br> | ||
| + | übrige sieben Teilnehmer auf restliche sieben Plätze verteilen: 7!<br> | ||
| + | (mit Reihenfolge, ohne Zurücklegen, Sonderfall: n=k)<br> | ||
| + | <math>\Rightarrow {4 \choose 2} \cdot 2! \cdot 7! = \underline {60.480}</math> | ||
| + | </popup> | ||
| Zeile 48: | Zeile 54: | ||
[[Bild:Stochastik04IV1b.jpg|750px]] | [[Bild:Stochastik04IV1b.jpg|750px]] | ||
}} | }} | ||
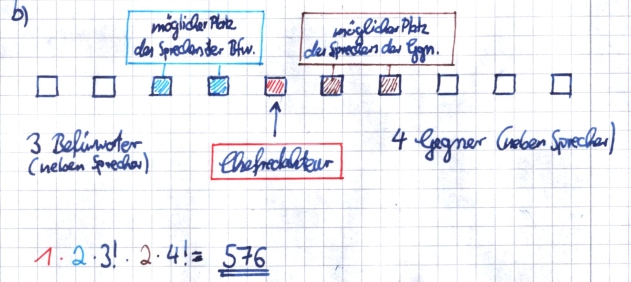
| + | <popup name="2. Lösung"> | ||
| + | ein Sprecher auf zwei Plätze verteilen: <math>{2 \choose 1}</math> gilt für zwei Sprecher: <math>\cdot 2</math><br> | ||
| + | übrige drei Befürworter auf drei Plätze links vom Chefredakteur verteilen: 3!<br> | ||
| + | übrige vier Gegner auf vier Plätze rechts vom Chefredakteur verteilen: 4!<br> | ||
| + | (beides mit Reihenfolge, ohne Zurücklegen, Sonderfall: n=k)<br> | ||
| + | <math>\Rightarrow {2 \choose 1} \cdot 2 \cdot 3! \cdot 4! = \underline {576}</math> | ||
| + | </popup> | ||
| Zeile 122: | Zeile 135: | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| − | [[Bild:Stochastik04IV3b.jpg|750px]] | + | [[Bild:Stochastik04IV3b.jpg|750px]]<br><br> |
| + | 2. Lösung | ||
| + | [[Bild:ABI_2004_VI_3b_Lös2.jpg|750px]] | ||
}} | }} | ||
| Zeile 137: | Zeile 152: | ||
;Aufgabe 4 | ;Aufgabe 4 | ||
| − | Ein großes Windparkunternehmen will sich durch Ausgabe von Aktien Kapital an der Börse verschaffen. Die Nachfrage ist | + | Ein großes Windparkunternehmen will sich durch Ausgabe von Aktien Kapital an der Börse verschaffen. Die Nachfrage ist erheblich; es werden wesentlich mehr Aktien geordert, als ausgegeben werden sollen. Daher erfolgt die Zuteilung im Losverfahren unter den Anlegern, die mindestens 200 Aktien geordert haben. Es werden nur Aktienpakete zu 50, 100 oder 200 Stück verlost. |
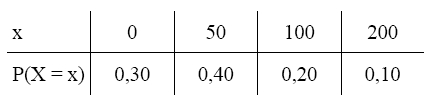
Die Zufallsgröße X, die die Anzahl der einem dieser Anleger zugeteilten Aktien beschreibt, hat die folgende Verteilung: | Die Zufallsgröße X, die die Anzahl der einem dieser Anleger zugeteilten Aktien beschreibt, hat die folgende Verteilung: | ||
Aktuelle Version vom 14. April 2010, 18:44 Uhr
|
|
|
Auf dem Gebiet der Gemeinde Windstätt soll ein Windpark zur Stromerzeugung errichtet werden. Die Gegner des Projekts befürchten eine Beeinträchtigung des Fremdenverkehrs und sammeln Unterschriften für ein Bürgerbegehren. Das Windstätter Tagblatt veranstaltet eine Podiumsdiskussion zum Thema Windpark.
An der Podiumsdiskussion nehmen neben dem Chefredakteur 5 Gegner und 4 Befürworter des Projekts teil. Die 10 Plätze auf dem Podium sind in einer Reihe nebeneinander angeordnet. Der Chefredakteur setzt sich auf den 5. Platz von links. Die beiden Gruppen haben jeweils einen Sprecher.
3BE
3BE
4BE
|
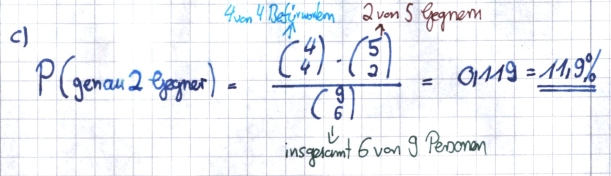
Im Verlauf der Podiumsdiskussion, zu der 178 Windstätter Bürger erschienen sind, behauptet der Sprecher der Windparkgegner, dass wenigstens 55% der mehr als 10 000 wahlberechtigten Gemeindemitglieder gegen das geplante Projekt sind.
6BE
2BE
|
Um den Ausgang des beantragten Bürgerentscheids zu prognostizieren, führte das Windstätter Tagblatt eine Umfrage unter 1200 wahlberechtigten Bürgern durch. Dabei sprachen sich 504 gegen das Projekt aus, während die übrigen 696 für die Errichtung des Windparks waren. a) Bestimmen Sie mithilfe der Ungleichung von Tschebyschow ein möglichst kleines Intervall, in dem der Anteil p der Windparkgegner unter allen Gemeindemitgliedern mit einer Wahrscheinlichkeit von wenigstens 75% liegt. Verwenden Sie p(p-1)<= 1/4. 5BE
6BE
|
Ein großes Windparkunternehmen will sich durch Ausgabe von Aktien Kapital an der Börse verschaffen. Die Nachfrage ist erheblich; es werden wesentlich mehr Aktien geordert, als ausgegeben werden sollen. Daher erfolgt die Zuteilung im Losverfahren unter den Anlegern, die mindestens 200 Aktien geordert haben. Es werden nur Aktienpakete zu 50, 100 oder 200 Stück verlost. Die Zufallsgröße X, die die Anzahl der einem dieser Anleger zugeteilten Aktien beschreibt, hat die folgende Verteilung: a) Berechnen Sie Erwartungswert und Standartabweichung von X. 4BE
7BE
|
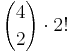
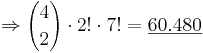
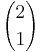 gilt für zwei Sprecher:
gilt für zwei Sprecher: