2009 II: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
(Grafik verkleinert) |
(BE eingefügt) |
||
| Zeile 29: | Zeile 29: | ||
| − | a) Untersuchen Sie am Funktionsterm das Verhalten von f<sub>a</sub> für x → −∞ und x → +∞. Begründen Sie, dass G<sub>a</sub> nie unterhalb der x-Achse verläuft. | + | a) Untersuchen Sie am Funktionsterm das Verhalten von f<sub>a</sub> für x → −∞ und x → +∞. Begründen Sie, dass G<sub>a</sub> nie unterhalb der x-Achse verläuft.<div align="right">''3 BE''</div> |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 38: | Zeile 38: | ||
| − | b) Bestimmen Sie Art und Lage der Extrempunkte von G<sub>a</sub>. [Zur Kontrolle: Tiefpunkt bei x = 0 und Hochpunkt bei x = <math>\textstyle \frac{2}{a}</math>] | + | b) Bestimmen Sie Art und Lage der Extrempunkte von G<sub>a</sub>. [Zur Kontrolle: Tiefpunkt bei x = 0 und Hochpunkt bei x = <math>\textstyle \frac{2}{a}</math>]<div align="right">''7 BE''</div> |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 59: | Zeile 59: | ||
Nun werden die in IR definierten Integralfunktionen <math>F_a : x \mapsto \int\limits_{0}^{x} f_a(t)dt</math> betrachtet. | Nun werden die in IR definierten Integralfunktionen <math>F_a : x \mapsto \int\limits_{0}^{x} f_a(t)dt</math> betrachtet. | ||
| − | a) Begründen Sie ohne Ausführung der Integration, dass der Graph von F<sub>a</sub> für alle a ∈ IR<sup>+</sup> durch den Koordinatenursprung verläuft und dort einen Terrassenpunkt besitzt. | + | a) Begründen Sie ohne Ausführung der Integration, dass der Graph von F<sub>a</sub> für alle a ∈ IR<sup>+</sup> durch den Koordinatenursprung verläuft und dort einen Terrassenpunkt besitzt.<div align="right">''4 BE''</div> |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 68: | Zeile 68: | ||
| − | b) Berechnen Sie durch partielle Integration einen integralfreien Term für F<sub>a</sub> . Geben Sie den Grenzwert von F<sub>a</sub> für x → +∞ an und interpretieren Sie das Ergebnis am Graphen G<sub>a</sub>. [Teilergebnis: F<sub>a</sub> = 2 - e<sup>-ax</sup> · (a<sup>2</sup>x<sup>2</sup> + 2ax + 2)] | + | b) Berechnen Sie durch partielle Integration einen integralfreien Term für F<sub>a</sub> . Geben Sie den Grenzwert von F<sub>a</sub> für x → +∞ an und interpretieren Sie das Ergebnis am Graphen G<sub>a</sub>. [Teilergebnis: F<sub>a</sub> = 2 - e<sup>-ax</sup> · (a<sup>2</sup>x<sup>2</sup> + 2ax + 2)]<div align="right">''10 BE''</div> |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 77: | Zeile 77: | ||
| − | c) Nun sei a = 0,04 . Der Graph der Funktion F<sub>0,04</sub> besitzt für x > 0 einen Wendepunkt W. Bestimmen Sie die Koordinaten von W. Skizzieren Sie unter Berücksichtigung der bisherigen Ergebnisse den Graphen von F<sub>0,04</sub> im Bereich − 30 ≤ x ≤ 200 in ein Koordinatensystem (x-Achse: 50 LE ≙ 2,5 cm, y-Achse: 1 LE ≙ 2,5 cm). Verwenden Sie dazu ohne Nachweis: F<sub>0,04</sub>(−30) ≈ −1,45 und F<sub>0,04</sub>(200) ≈1,97 . | + | c) Nun sei a = 0,04 . Der Graph der Funktion F<sub>0,04</sub> besitzt für x > 0 einen Wendepunkt W. Bestimmen Sie die Koordinaten von W. Skizzieren Sie unter Berücksichtigung der bisherigen Ergebnisse den Graphen von F<sub>0,04</sub> im Bereich − 30 ≤ x ≤ 200 in ein Koordinatensystem (x-Achse: 50 LE ≙ 2,5 cm, y-Achse: 1 LE ≙ 2,5 cm). Verwenden Sie dazu ohne Nachweis: F<sub>0,04</sub>(−30) ≈ −1,45 und F<sub>0,04</sub>(200) ≈1,97 .<div align="right">''6 BE''</div> |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 100: | Zeile 100: | ||
| − | a) Bestimmen Sie die Parameter a und k, wenn das Maximum der Funktion g um 18.50 Uhr auftritt und 26 Besucher pro Minute beträgt. | + | a) Bestimmen Sie die Parameter a und k, wenn das Maximum der Funktion g um 18.50 Uhr auftritt und 26 Besucher pro Minute beträgt.<div align="right">''5 BE''</div> |
| − | b) Berechnen Sie für a = 0,04 und k = 1200 unter Verwendung des in Teilaufgabe 2b ermittelten Terms F<sub>a</sub> (x) das Integral <math> \int\limits_{0}^{120} g(x)dx</math> und interpretieren Sie das Ergebnis im Anwendungszusammenhang. | + | b) Berechnen Sie für a = 0,04 und k = 1200 unter Verwendung des in Teilaufgabe 2b ermittelten Terms F<sub>a</sub> (x) das Integral <math> \int\limits_{0}^{120} g(x)dx</math> und interpretieren Sie das Ergebnis im Anwendungszusammenhang.<div align="right">''5 BE''</div> |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
Version vom 29. März 2010, 14:11 Uhr
|
|
Gegeben ist die Schar der Funktionen
3 BE
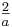 ] ]7 BE
|
Nun werden die in IR definierten Integralfunktionen 4 BE
10 BE
6 BE
|
Die Gruppe „Die toten Rosen“ gibt ein Konzert. Es beginnt um 20 Uhr, der Einlass wird ab 18 Uhr gewährt. Der Besucherzustrom soll durch eine Funktion g der Form g(x) = k ⋅ fa (x) mit geeignetem a und geeignetem k > 0 modelliert werden. Dabei bedeutet x die seit 18 Uhr vergangene Zeit in Minuten. g(x) gibt die momentane Zunahme der Besucherzahl in Besucher pro Minute an.
5 BE
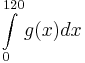 und interpretieren Sie das Ergebnis im Anwendungszusammenhang. und interpretieren Sie das Ergebnis im Anwendungszusammenhang.5 BE
|
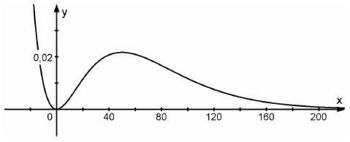
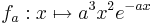 mit a ∈ IR+ und der Definitionsmenge IR . Der Graph von fa wird mit Ga bezeichnet. Die Abbildung zeigt Ga für a = 0,04.
mit a ∈ IR+ und der Definitionsmenge IR . Der Graph von fa wird mit Ga bezeichnet. Die Abbildung zeigt Ga für a = 0,04.
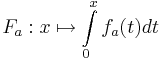 betrachtet.
betrachtet.

