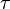2005 VI: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: <div style="padding:1px;background: #EEEEE6;border:0px groove;"> <center><table border="0" width="800px" cellpadding=5 cellspacing=15> <tr><td width="800px" valign="t...) |
|||
| Zeile 24: | Zeile 24: | ||
In einem kartesischen Koordinatensystem ist die Geradenschar | In einem kartesischen Koordinatensystem ist die Geradenschar | ||
| − | g<sub>a</sub> : <math>\vec x = \begin{pmatrix} 4 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot\begin{pmatrix} a \\ 1 \\ a+2 \end{pmatrix}</math> mit a, <math>\lambda</math> <math>\in</math> <math>\mathbb{R} </math><sup>-</sup> gegeben.Die Punkte A(10/0/0), B(0/5/0) und C(0/0/5) bestimmen eine Ebene, die mit E bezeichnet wird. | + | g<sub>a</sub> : <math>\vec x = \begin{pmatrix} 4 \\ 2 \\ 1 \end{pmatrix} + \lambda \cdot\begin{pmatrix} a \\ 1 \\ a+2 \end{pmatrix}</math> |
| + | mit a, <math>\lambda</math> <math>\in</math> <math>\mathbb{R}</math><sup>-</sup> gegeben. Die Punkte A(10/0/0), B(0/5/0) und C(0/0/5) bestimmen eine Ebene, die mit E bezeichnet wird. | ||
</td></tr></table></center> | </td></tr></table></center> | ||
Version vom 21. März 2010, 15:08 Uhr
|
|
|
In einem kartesischen Koordinatensystem ist die Geradenschar
ga : |
a) Ermitteln Sie eine Gleichung der Ebene E in Normalenform. [mögliches Ergebnis E: x1 + 2x2 + 2x3 - 10 = 0] 3 BE
3 BE
4 BE
|
a) Der Punkt C wird an der Geraden AB gespiegelt. Ermitteln Sie die Koordinaten des Spiegelpunkts C*. [Ergebnis: C* = (4/8/-5)] 5 BE
4 BE
6 BE
|
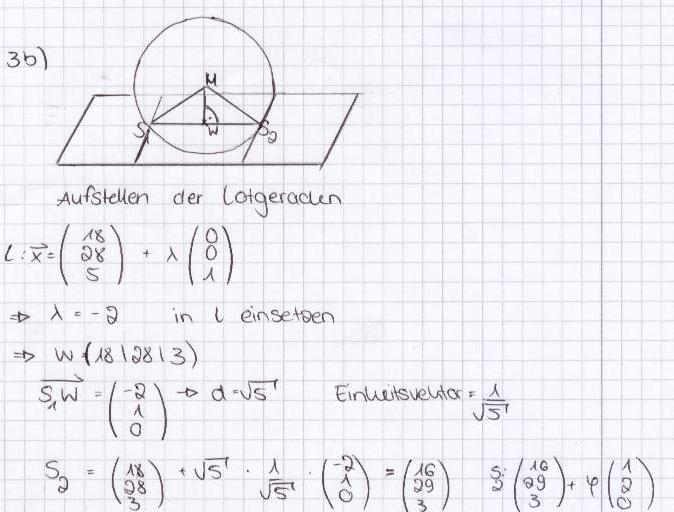
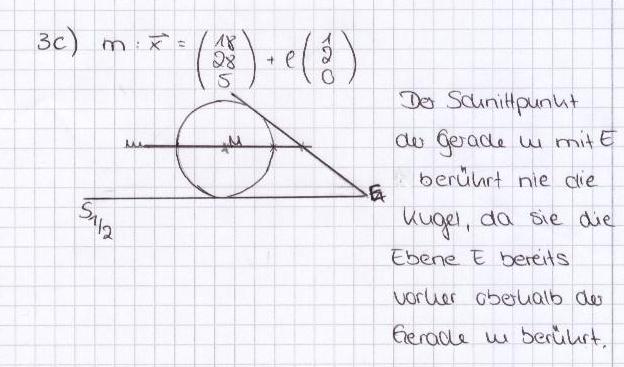
In der Ebene H: x3 = 3 liegen zwei parallele Schienen s1 und s2.Die Schiene s1 wird durch die Gerade s1 : a) Berechnen Sie die Koordinaten des Punkts S, in dem die Kugel die Schiene s1 berührt. [Ergebnis: S = (20/27/3)] 6 BE
5 BE
4 BE
|
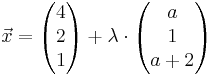 mit a,
mit a, 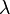

 - gegeben. Die Punkte A(10/0/0), B(0/5/0) und C(0/0/5) bestimmen eine Ebene, die mit E bezeichnet wird.
- gegeben. Die Punkte A(10/0/0), B(0/5/0) und C(0/0/5) bestimmen eine Ebene, die mit E bezeichnet wird.




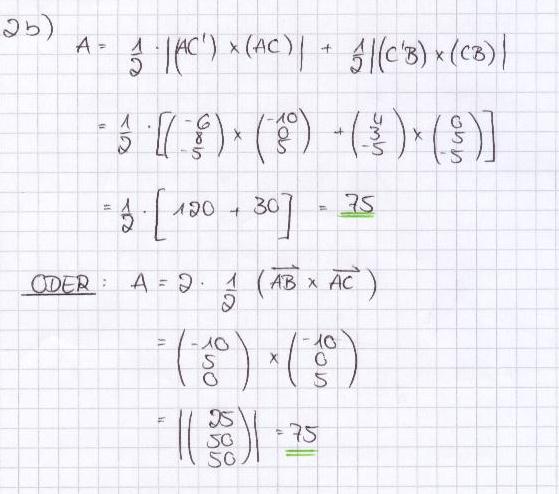

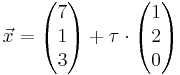 mit
mit