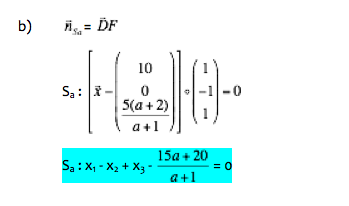2006 VI: Unterschied zwischen den Versionen
| Zeile 12: | Zeile 12: | ||
| − | <center>Erarbeitet von Lisa Köhler</center> | + | <center>Erarbeitet von Lisa Köhler, Sebastian Schirmer</center> |
</td></tr></table></center> | </td></tr></table></center> | ||
| Zeile 44: | Zeile 44: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| + | [[Bild:Abi2006,1b.png|600px]]<br /> | ||
[[Bild:Abi2006,1b.png|600px]] | [[Bild:Abi2006,1b.png|600px]] | ||
}}<br /> | }}<br /> | ||
Version vom 18. März 2010, 19:04 Uhr
|
|
Gegeben ist eine Kugel K mit dem Radius 5, die in eine im Koordinatensystem stehende würfelförmige Schachtel ABCDEFGH mit der Kantenlänge 10 (siehe Abbildung) verpackt ist, sowie die Punkteschar
Pa(10|0|
b) Berechnen Sie die Koordinaten der Punkte Z1 und Z2 , in denen die Gerade DF die Kugel schneidet. (5 BE)
c) Geben Sie die kürzeste Strecke an, auf der sich der Punkt Pa bewegt, wenn a das Intervall [0;∞[ durchläuft. Begründen Sie Ihre Antwort. (5 BE)
|
Um diese Verpackung attraktiver zu gestalten, werden durch Ebenen, die senkrecht zu den Raumdiagonalen des Würfels verlaufen, an allen seinen Ecken kongruente dreiseitige Pyramiden abgeschnitten. a) Um welche besonderen Dreiecke handelt es sich bei der Grundfläche (Schnittfläche) und den Seitenflächen der abgeschnittenen Pyramiden? (3 BE)
|
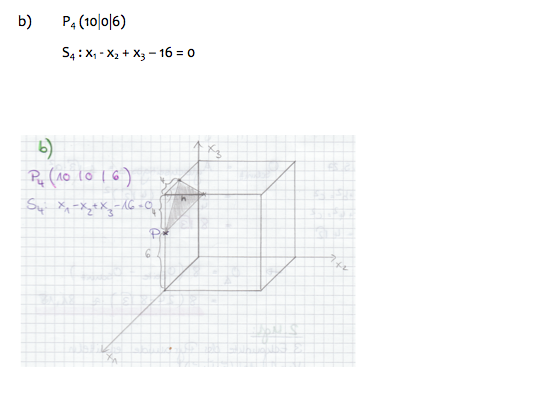
Im Folgenden sei a = 4. a) Zeigen Sie durch Rechnung, dass die Ebene S4 die Kugel nicht
schneidet. (5 BE)
|
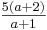 ) mit dem Parameter a ∈ IR0+.
) mit dem Parameter a ∈ IR0+. 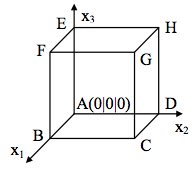

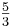
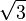 |5-
|5-


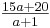 = 0]
= 0]