2006 V: Unterschied zwischen den Versionen
| Zeile 81: | Zeile 81: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| − | Die Ebene E ist Tangentialebene an zwei | + | Die Ebene E ist Tangentialebene an zwei Kugeln K<sub>1</sub> und K<sub>2</sub> mit dem Radius <math>5\sqrt{2}</math>, deren Mittelpunkte M<sub>1</sub> und M<sub>2</sub> auf der Gerade h liegen. |
a) Bestimmen Sie die Koordinaten von M<sub>1</sub> und M<sub>2</sub> . (Der Punkt mit ausschließlich ganzzahligen Koordinaten wird mit M<sub>1</sub> bezeichnet.) | a) Bestimmen Sie die Koordinaten von M<sub>1</sub> und M<sub>2</sub> . (Der Punkt mit ausschließlich ganzzahligen Koordinaten wird mit M<sub>1</sub> bezeichnet.) | ||
| − | [Teilergebnis: (2/5/-6)] | + | [Teilergebnis: M<sub>1</sub> = (2/5/-6)] |
<div align="right"><i>'''6 BE'''</i></div> | <div align="right"><i>'''6 BE'''</i></div> | ||
Version vom 26. Februar 2010, 13:41 Uhr
|
|
|
In einem kartesischen Koordinatensystem des
|
 3 ist die
Ebene E: x2 - x3 - 1 = 0 , die Geradenschar gk :
3 ist die
Ebene E: x2 - x3 - 1 = 0 , die Geradenschar gk : 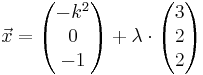 und die Gerade h :
und die Gerade h : 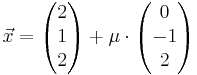 gegeben, wobei k,
gegeben, wobei k, 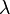 und
und 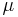 aus
aus 

 /
/ ) ]
) ]

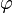 zwischen hE und h in Grad auf eine Nachkommastelle gerundet.
zwischen hE und h in Grad auf eine Nachkommastelle gerundet.

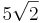 , deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
, deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
 K1 und Q
K1 und Q 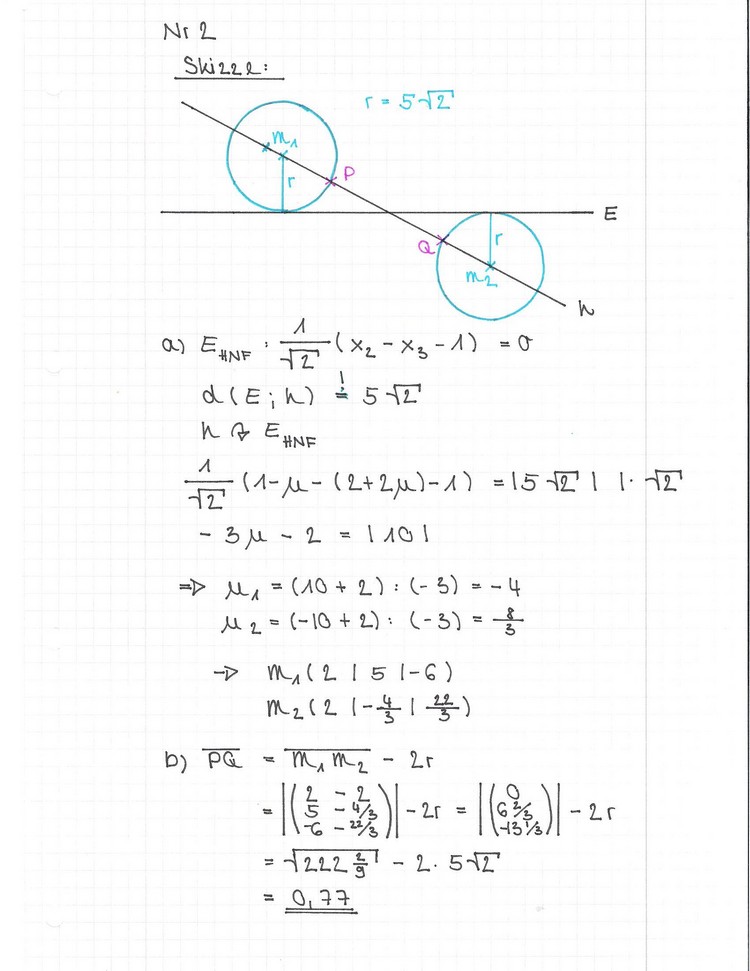
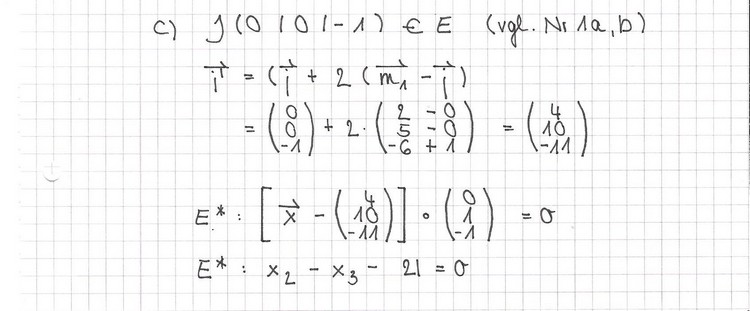

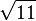 ]
]