2006 V: Unterschied zwischen den Versionen
| Zeile 24: | Zeile 24: | ||
<tr><td width="800px" valign="top"> | <tr><td width="800px" valign="top"> | ||
| − | |||
In einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> ist die | In einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> ist die | ||
Ebene E: x<sub>2</sub> - x<sub>3</sub> - 1 = 0 , die Geradenschar g<sub>k</sub> : <math>\vec x = \begin{pmatrix} -k^2 \\ 0 \\ -1 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}</math> und die Gerade h : <math>\vec x = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} + \mu \cdot\begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix}</math> gegeben, wobei k, <math>\lambda</math> und <math>\mu</math> aus <math>\mathbb{R} </math> sind. | Ebene E: x<sub>2</sub> - x<sub>3</sub> - 1 = 0 , die Geradenschar g<sub>k</sub> : <math>\vec x = \begin{pmatrix} -k^2 \\ 0 \\ -1 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}</math> und die Gerade h : <math>\vec x = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} + \mu \cdot\begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix}</math> gegeben, wobei k, <math>\lambda</math> und <math>\mu</math> aus <math>\mathbb{R} </math> sind. | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 1 | ||
a) Zeigen Sie: Alle Geraden der Schar g<sub>k</sub> sind zueinander parallel und liegen in der Ebene E. | a) Zeigen Sie: Alle Geraden der Schar g<sub>k</sub> sind zueinander parallel und liegen in der Ebene E. | ||
Version vom 25. Februar 2010, 14:46 Uhr
|
|
|
In einem kartesischen Koordinatensystem des
|
 3 ist die
Ebene E: x2 - x3 - 1 = 0 , die Geradenschar gk :
3 ist die
Ebene E: x2 - x3 - 1 = 0 , die Geradenschar gk : 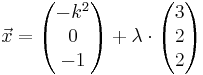 und die Gerade h :
und die Gerade h : 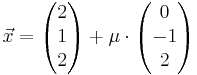 gegeben, wobei k,
gegeben, wobei k, 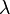 und
und 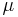 aus
aus  /
/ ) ]
) ]
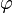 zwischen hE und h in Grad auf eine Nachkommastelle gerundet.
zwischen hE und h in Grad auf eine Nachkommastelle gerundet.
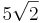 , deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
, deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
 K1 und Q
K1 und Q 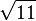 ]
]

