2006 V: Unterschied zwischen den Versionen
| Zeile 25: | Zeile 25: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| − | In einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> die | + | In einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> ist die |
Ebene E: x<sub>2</sub> - x<sub>3</sub> - 1 = 0 , die Geradenschar g<sub>k</sub> : <math>\vec x = \begin{pmatrix} -k^2 \\ 0 \\ -1 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}</math> und die Gerade h : <math>\vec x = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} + \mu \cdot\begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix}</math> gegeben, wobei k, <math>\lambda</math> und <math>\mu</math> aus <math>\mathbb{R} </math> sind. | Ebene E: x<sub>2</sub> - x<sub>3</sub> - 1 = 0 , die Geradenschar g<sub>k</sub> : <math>\vec x = \begin{pmatrix} -k^2 \\ 0 \\ -1 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}</math> und die Gerade h : <math>\vec x = \begin{pmatrix} 2 \\ 1 \\ 2 \end{pmatrix} + \mu \cdot\begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix}</math> gegeben, wobei k, <math>\lambda</math> und <math>\mu</math> aus <math>\mathbb{R} </math> sind. | ||
a) Zeigen Sie: Alle Geraden der Schar g<sub>k</sub> sind zueinander parallel und liegen in der Ebene E. | a) Zeigen Sie: Alle Geraden der Schar g<sub>k</sub> sind zueinander parallel und liegen in der Ebene E. | ||
| + | |||
| + | <div align="right"><i>'''3 BE'''</i></div> | ||
| + | <br> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| Zeile 35: | Zeile 38: | ||
b) Begründen Sie, dass die Schar der Geraden g<sub>k</sub> eine Halbebene von E bildet. | b) Begründen Sie, dass die Schar der Geraden g<sub>k</sub> eine Halbebene von E bildet. | ||
| + | |||
| + | <div align="right"><i>'''4 BE'''</i></div> | ||
| + | <br> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| Zeile 44: | Zeile 50: | ||
[ Teilergebnis: (2/<math>\frac{5}{3}</math>/<math>\frac{2}{3}</math>) ] | [ Teilergebnis: (2/<math>\frac{5}{3}</math>/<math>\frac{2}{3}</math>) ] | ||
| + | <div align="right"><i>'''5 BE'''</i></div> | ||
| + | <br> | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | . | ||
| + | }} | ||
| + | |||
| + | d) Projiziert man h senkrecht auf E, so erhält man die Gerade h<sub>E</sub>. Berechnen Sie den Winkel <math>\varphi</math> zwischen h<sub>E</sub> und h in Grad auf eine Nachkommastelle gerundet. | ||
| + | |||
| + | <div align="right"><i>'''5 BE'''</i></div> | ||
| + | <br> | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | . | ||
| + | }} | ||
</div> | </div> | ||
| Zeile 55: | Zeile 76: | ||
Die Ebene E ist Tangentialebene an zwei Kukeln K<sub>1</sub> und K<sub>2</sub> mit dem Radius <math>5\sqrt{2}</math>, deren Mittelpunkte M<sub>1</sub> und M<sub>2</sub> auf der Gerade h liegen. | Die Ebene E ist Tangentialebene an zwei Kukeln K<sub>1</sub> und K<sub>2</sub> mit dem Radius <math>5\sqrt{2}</math>, deren Mittelpunkte M<sub>1</sub> und M<sub>2</sub> auf der Gerade h liegen. | ||
| − | a) | + | a)Bestimmen Sie die Koordinaten von M<sub>1</sub> und M<sub>2</sub> . (Der Punkt mit ausschließlich ganzzahligen Koordinaten wird mit M<sub>1</sub> bezeichnet.) |
| + | [Teilergebnis: (2/5/-6)] | ||
| + | |||
| + | <div align="right"><i>'''6 BE'''</i></div> | ||
| + | <br> | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | . | ||
| + | }} | ||
| + | |||
| + | b) Die Kugelpunkte P <math>\in</math> K<sub>1</sub> und Q <math>\in \in</math> K<sub>2</sub> sind diejenigen Punkte, die minimale Distanz voneinander haben. Berechnen Sie die Entfernung [PQ] auf zwei Dezimalen gerundet. | ||
| + | |||
| + | <div align="right"><i>'''3 BE'''</i></div> | ||
| + | <br> | ||
| + | |||
| + | :{{Lösung versteckt| | ||
| + | . | ||
| + | }} | ||
| + | |||
| + | |||
Version vom 25. Februar 2010, 14:29 Uhr
|
|
In einem kartesischen Koordinatensystem des a) Zeigen Sie: Alle Geraden der Schar gk sind zueinander parallel und liegen in der Ebene E. 3 BE
. b) Begründen Sie, dass die Schar der Geraden gk eine Halbebene von E bildet. 4 BE
. c) Für welche Werte von k schneidet gk die Gerade h? Ermitteln Sie die Koordinaten des Schnittpunkts S. [ Teilergebnis: (2/ 5 BE
. d) Projiziert man h senkrecht auf E, so erhält man die Gerade hE. Berechnen Sie den Winkel 5 BE
. </div>
Fehler beim Parsen(Syntaxfehler): \left( -k |
 3 ist die
Ebene E: x2 - x3 - 1 = 0 , die Geradenschar gk :
3 ist die
Ebene E: x2 - x3 - 1 = 0 , die Geradenschar gk : 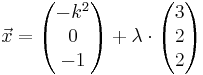 und die Gerade h :
und die Gerade h : 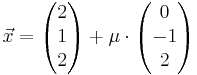 gegeben, wobei k,
gegeben, wobei k, 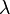 und
und 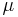 aus
aus  /
/ ) ]
) ]
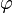 zwischen hE und h in Grad auf eine Nachkommastelle gerundet.
zwischen hE und h in Grad auf eine Nachkommastelle gerundet.
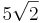 , deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
, deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
 K1 und Q
K1 und Q 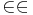 K2 sind diejenigen Punkte, die minimale Distanz voneinander haben. Berechnen Sie die Entfernung [PQ] auf zwei Dezimalen gerundet.
K2 sind diejenigen Punkte, die minimale Distanz voneinander haben. Berechnen Sie die Entfernung [PQ] auf zwei Dezimalen gerundet.

