2006 V: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
| Zeile 25: | Zeile 25: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| + | In einem kartesischen Koordinatensystem des IR<sup>3</sup>sind die | ||
| + | Ebene E: x<sub>2</sub> - x<sub>3</sub> - 1 = 0 , die Geradenschar g<sub>k</sub> : <math>\vec x = \begin{pmatrix} -k<sup>2</sup> \\ 0 \\ -1 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 3 \\ 2 \\ 2 \end{pmatrix}</math> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | + | . | |
}} | }} | ||
| Zeile 44: | Zeile 46: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | Die Ebene E ist Tangentialebene an zwei Kukeln K<sub>1</sub> und K<sub>2</sub> mit dem Radius <math>5\sqrt{2}</math>, deren Mittelpunkte M<sub>1</sub> und M<sub>2</sub> auf der Gerade h liegen. | ||
| − | + | a) | |
| Zeile 54: | Zeile 57: | ||
</div> | </div> | ||
| + | <math>\left( -k</math> | ||
Version vom 25. Februar 2010, 11:21 Uhr
|
|
In einem kartesischen Koordinatensystem des IR3sind die
Ebene E: x2 - x3 - 1 = 0 , die Geradenschar gk :
.
|
Die Ebene E ist Tangentialebene an zwei Kukeln K1 und K2 mit dem Radius a)
|
Fehler beim Parsen(Syntaxfehler): \left( -k
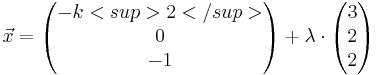
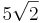 , deren Mittelpunkte M1 und M2 auf der Gerade h liegen.
, deren Mittelpunkte M1 und M2 auf der Gerade h liegen.

