2007 V: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
(Abituraufgabe_2007_Anfang) |
(Abiaufgabe) |
||
| Zeile 37: | Zeile 37: | ||
[mögliches Teilergebnis: g: <math>\vec x = \begin{pmatrix} 1 \\ 2 \\ -3 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 1 \\ 1 \\ -3 \end{pmatrix}</math>, λ ∈ IR ] | [mögliches Teilergebnis: g: <math>\vec x = \begin{pmatrix} 1 \\ 2 \\ -3 \end{pmatrix} + \lambda \cdot\begin{pmatrix} 1 \\ 1 \\ -3 \end{pmatrix}</math>, λ ∈ IR ] | ||
| − | + | :;1. Lösungsweg: | |
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:Aufgabe_1_b_Loesung_I.jpg|800px]] | [[Bild:Aufgabe_1_b_Loesung_I.jpg|800px]] | ||
| + | }} | ||
| + | :;2. Lösungsweg: | ||
| + | :{{Lösung versteckt|1= | ||
| + | [[Bild:Aufgabe_1_b_Loesung_II.jpg|800px]] | ||
}} | }} | ||
Version vom 17. Februar 2010, 21:05 Uhr
|
|
Gegeben ist in einem kartesischen Koordinatensystem des IR3 die Ebenenschar Ek : k2x1 + k 2x2 - k2 = 0 , mit k ∈ IR als Scharparameter.
b) Die beiden Ebenen E2 und E-3 schneiden sich in einer Geraden g. Ermitteln Sie eine Gleichung von g in Parameterform und den der beiden Ebenen auf eine Dezimale gerundet. [mögliches Teilergebnis: g:
|

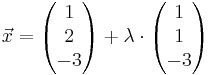 , λ ∈ IR ]
, λ ∈ IR ]



