2008 I: Unterschied zwischen den Versionen
K |
(layout) |
||
| (6 dazwischenliegende Versionen von 2 Benutzern werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | |
| − | + | ||
| − | == | + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> |
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | <center><big>'''Leistungskurs Mathematik (Bayern): Abiturprüfung 2008'''</big></center> | ||
| + | <center><big>'''Infinitesimalrechnung I'''</big></center> | ||
| + | |||
| + | |||
| + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=6765c5a90ce67dce2877992c3f4e2d9f '''Download der Originalaufgaben: Abitur 2008 LK Mathematik Bayern'''] - [[Media:LKM Abi 2008 I lös neu.doc|Lösung gesamt]] | ||
| + | <br />Erarbeitet von Sebastian Waldhäuser & Daniel Greb</center> | ||
| + | |||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 1 | ||
Gegeben ist die Funktion <math>f:x\rightarrow \frac{ln(x^2)}{x}</math> D<sub>f</sub> = IR \ {0}. Der Graph von f | Gegeben ist die Funktion <math>f:x\rightarrow \frac{ln(x^2)}{x}</math> D<sub>f</sub> = IR \ {0}. Der Graph von f | ||
| Zeile 26: | Zeile 45: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild:ABI_2008_I_1bSkizze_Lös.jpg]] | + | [[Bild:ABI_2008_I_1bSkizze_Lös.jpg|750px]] |
}} | }} | ||
| − | c) Zeigen Sie, dass für alle u >1 gilt: <math>\int_{\frac{1}{u} }^{u} f(x)\,dx=0</math> . Interpretieren Sie das Ergebnis der Integration am Graphen von f. (7 BE) | + | c) Zeigen Sie, dass für alle u >1 gilt: <math>\int_{\frac{1}{u} }^{u} f(x)\,dx=0</math> . Interpretieren Sie das Ergebnis der Integration am Graphen von f. (7 BE)<br /> |
| + | <popup name="Bemerkung"> | ||
| + | * Die folgende Überlegung gilt nur für x>0! | ||
| + | |||
| + | </popup><br /> | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| Zeile 41: | Zeile 64: | ||
}} | }} | ||
| − | == | + | </td></tr></table></center> |
| + | |||
| + | |||
| + | </div> | ||
| + | |||
| + | <div style="padding:1px;background: #EEEEE6;border:0px groove;"> | ||
| + | |||
| + | <center><table border="0" width="800px" cellpadding=5 cellspacing=15> | ||
| + | <tr><td width="800px" valign="top"> | ||
| + | |||
| + | ;Aufgabe 2 | ||
Betrachtet wird die Funktion K mit dem Term <math>K(v)=\frac{v}{\frac{v^2}{2a}+tv+s }</math>, v ∈ IR<sup>+</sup>, und den positiven Parametern a, t und s. | Betrachtet wird die Funktion K mit dem Term <math>K(v)=\frac{v}{\frac{v^2}{2a}+tv+s }</math>, v ∈ IR<sup>+</sup>, und den positiven Parametern a, t und s. | ||
| Zeile 72: | Zeile 105: | ||
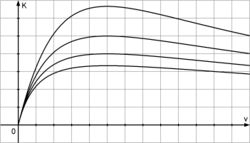
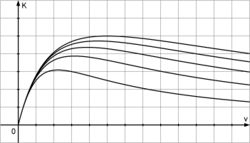
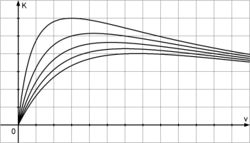
<br />Diagramme: <br /> | <br />Diagramme: <br /> | ||
| − | + | I II III | |
| − | + | ||
| − | + | [[Bild:ABI_2008_I_2d_I.jpg|250px]] | |
| − | [[Bild:ABI_2008_I_2d_II.jpg| | + | [[Bild:ABI_2008_I_2d_II.jpg|250px]] |
| − | + | [[Bild:ABI_2008_I_2d_III.jpg|250px]] | |
| − | + | ||
| − | [[Bild:ABI_2008_I_2d_III.jpg| | + | |
| Zeile 86: | Zeile 116: | ||
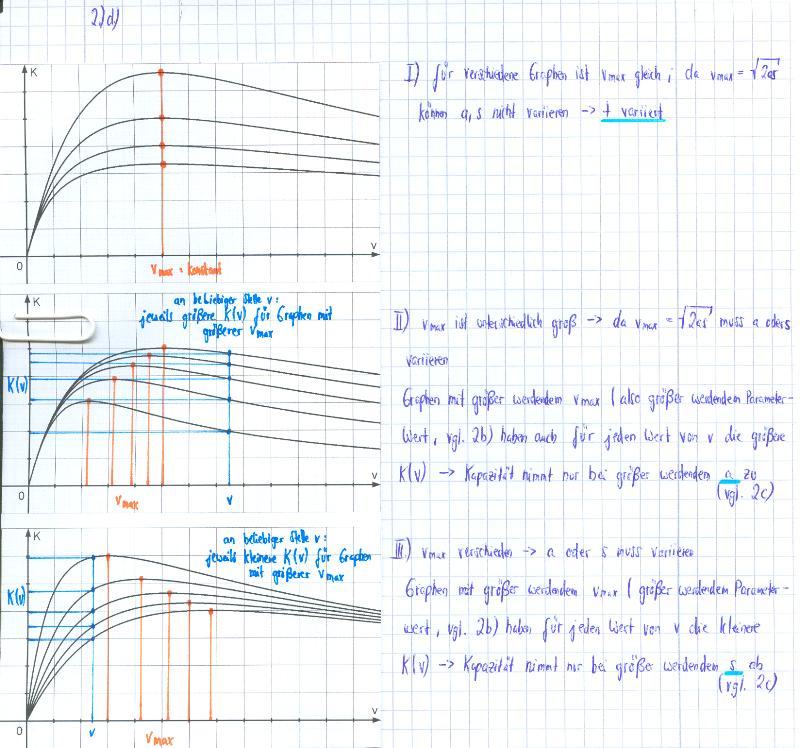
[[Bild:ABI_2008_I_2d_Lös.jpg]] | [[Bild:ABI_2008_I_2d_Lös.jpg]] | ||
}} | }} | ||
| + | </td></tr></table></center> | ||
| + | |||
| + | |||
| + | </div> | ||
Aktuelle Version vom 17. Februar 2010, 11:21 Uhr
|
Erarbeitet von Sebastian Waldhäuser & Daniel Greb |
Gegeben ist die Funktion a) Untersuchen Sie das Symmetrieverhalten von Gf. Bestimmen Sie die Nullstellen von f und das Verhalten von f an den Rändern des Definitionsbereichs. (6 BE)
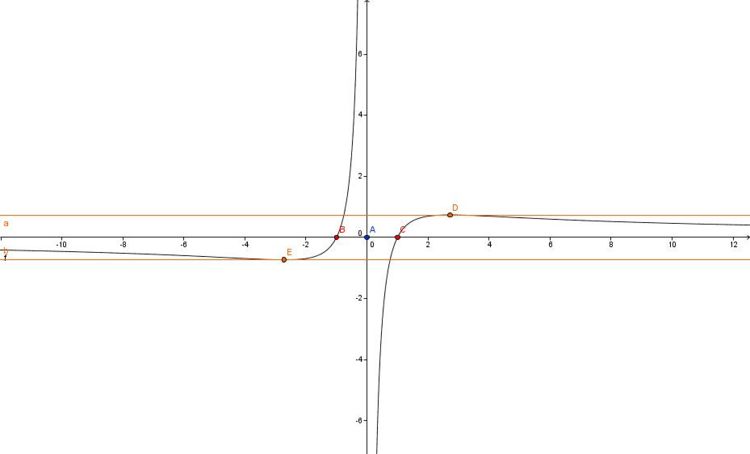
Skizze c) Zeigen Sie, dass für alle u >1 gilt: Skizze |
Betrachtet wird die Funktion K mit dem Term a)Bestimmen Sie die Grenzwerte von
I II III
|
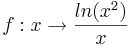 Df = IR \ {0}. Der Graph von f
wird mit Gf bezeichnet.
Df = IR \ {0}. Der Graph von f
wird mit Gf bezeichnet.


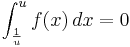 . Interpretieren Sie das Ergebnis der Integration am Graphen von f. (7 BE)
. Interpretieren Sie das Ergebnis der Integration am Graphen von f. (7 BE)
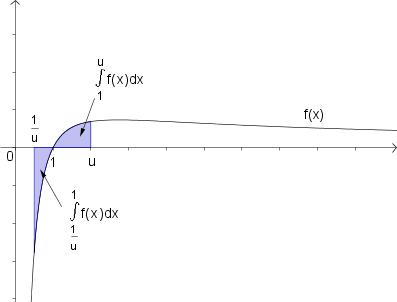
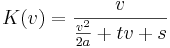 , v ∈ IR+, und den positiven Parametern a, t und s.
K beschreibt in einem idealisierten Modell die sogenannte Kapazität einspuriger Straßen, das ist die Anzahl der Fahrzeuge, die bei genauer Einhaltung des Sicherheitsabstandes pro Zeiteinheit eine bestimmte Stelle passieren können. In diesem Modell wird vereinfachend angenommen, dass alle Fahrzeuge mit der gleichen Geschwindigkeit v fahren und außerdem die Parameter a (Bremsverzögerung), t (Reaktionszeit des Fahrers) und s (Fahrzeuglänge) für alle Fahrzeuge der Kolonne gleich sind.
, v ∈ IR+, und den positiven Parametern a, t und s.
K beschreibt in einem idealisierten Modell die sogenannte Kapazität einspuriger Straßen, das ist die Anzahl der Fahrzeuge, die bei genauer Einhaltung des Sicherheitsabstandes pro Zeiteinheit eine bestimmte Stelle passieren können. In diesem Modell wird vereinfachend angenommen, dass alle Fahrzeuge mit der gleichen Geschwindigkeit v fahren und außerdem die Parameter a (Bremsverzögerung), t (Reaktionszeit des Fahrers) und s (Fahrzeuglänge) für alle Fahrzeuge der Kolonne gleich sind.
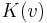 für
für 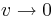 und
und 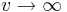 . (3 BE)
. (3 BE)

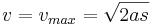 maxmal wird. Berechnen sie
maxmal wird. Berechnen sie 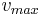 in
in 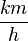 für
für 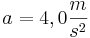 (Regennasse Fahrbahn)und
(Regennasse Fahrbahn)und 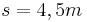 . (8 BE)
. (8 BE)