2008 V: Unterschied zwischen den Versionen
| Zeile 10: | Zeile 10: | ||
| − | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID= | + | <center>[http://www.isb.bayern.de/isb/download.aspx?DownloadFileID=6765c5a90ce67dce2877992c3f4e2d9f '''Download der Originalaufgaben: Abitur 2008 LK Mathematik Bayern'''] - [[Media:LKM Abi 2008 V lös.doc|Lösungen zum Ausdrucken]]</center> |
</td></tr></table></center> | </td></tr></table></center> | ||
Version vom 9. Februar 2010, 10:37 Uhr
|
|
|
1) a) Zeigen Sie, dass die Punkte A, B und D eine Ebene E bestimmen, und ermitteln Sie eine Gleichung der Ebene E in Normalenform. (5 BE) Zur Kontrolle: E: 2x1+2x2+x3-9=0 b) Weisen Sie nach, dass sich die Punkte A, B und D durch einen vierten Punkt C zu einem Quadrat ABCD ergänzen lassen, und berechnen Sie den Diagonalenschnittpunkt M dieses Quadrats. (4 BE) Teilergebnis: M(2|3|-1) c) Für welchen Wert von t ist die Entfernung von St zu M minimal? (5 BE) 2) Das Quadrat ABCD als Begrenzungsfläche und die Strecke [DSt] als Seitenkante bestimmen ein Parallelflach. a) Berechnen Sie alle Werte von t, für die das Parallelflach den Rauminhalt V=144 hat. (6 BE) b) Bestimmen Sie t so, dass das Parallelflach ein Quader ist. (3 BE) Nun sei t=1. Die durch die Punkte A, D und S1 festgelegte Seitenfläche des Parallelflachs liegt in der Ebene F:2x1-x3+1=0. c) Im Punkt T(1|5|3) dieser Seitenfläche wird ein Lot errichtet. Berechnen Sie die Koordinaten des Punktes U, in dem das Lot die Ebene E schneidet, und zeigen Sie, dass U nicht im Innern des Quadrats ABCD liegt.(7 BE) d) Ermitteln Sie den Schnittwinkel der Ebenen E und F. (3 BE) |
 3 die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie St (1-t|8|t) mit
3 die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie St (1-t|8|t) mit 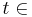 {9} als Parameter.
{9} als Parameter.

