2008 V: Unterschied zwischen den Versionen
Aus RMG-Wiki
< LK Mathematik | Abitur
| Zeile 3: | Zeile 3: | ||
Gegeben sind in einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie S<sub>t</sub> (1-t|8|t) mit <math>t \in</math> {9} als Parameter. | Gegeben sind in einem kartesischen Koordinatensystem des <math>\mathbb{R} </math><sup>3</sup> die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie S<sub>t</sub> (1-t|8|t) mit <math>t \in</math> {9} als Parameter. | ||
| + | |||
| + | 1) a) Zeigen Sie, dass die Punkte A, B und D eine Ebene E bestimmen, und ermitteln Sie eine Gleichung der Ebene E in Normalenform. ''(5 BE)'' | ||
| + | |||
| + | Zur Kontrolle: E: 2x<sub>1</sub>+2x<sub>2</sub>+x<sub>3</sub>-9=0 | ||
| + | |||
| + | b) Weisen Sie nach, dass sich die Punkte A, B und D durch einen vierten Punkt C zu einem Quadrat ABCD ergänzen lassen, und berechnen Sie den Diagonalenschnittpunkt M dieses Quadrats. | ||
| + | |||
| + | Teilergebnis: M(2|3|-1) | ||
Version vom 9. Februar 2010, 10:25 Uhr
Inhalt folgt
Gegeben sind in einem kartesischen Koordinatensystem des 
3 die Punkte A(1|2|3), B(5|0|-1) und D(-1|6|-1) sowie St (1-t|8|t) mit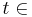 
{9} als Parameter.
1) a) Zeigen Sie, dass die Punkte A, B und D eine Ebene E bestimmen, und ermitteln Sie eine Gleichung der Ebene E in Normalenform. (5 BE)
Zur Kontrolle: E: 2x1+2x2+x3-9=0
b) Weisen Sie nach, dass sich die Punkte A, B und D durch einen vierten Punkt C zu einem Quadrat ABCD ergänzen lassen, und berechnen Sie den Diagonalenschnittpunkt M dieses Quadrats.
Teilergebnis: M(2|3|-1)
