Übungsaufgaben
Aufgabe 1:
Beschreibe, wie die unten abgebildeten Funktionen aus den vorangegangen Funktionen entstanden sind.
Ausgangsfunktion
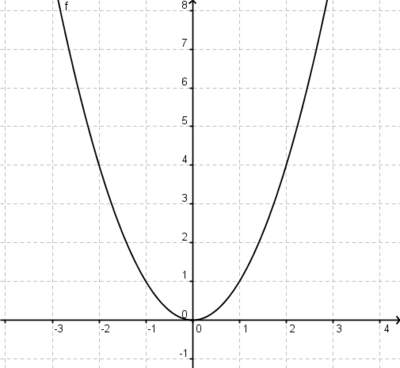
Beispiel:
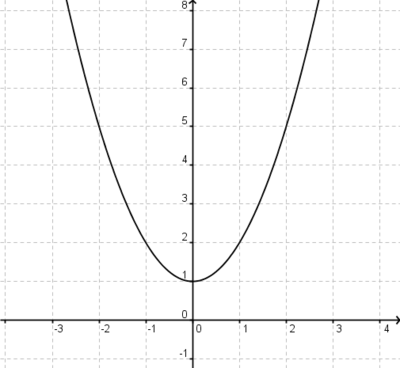
Verschiebung um 1 Einheit in positiver y-Richtung
Diese Funktion dient nun als Ausgangsfunktion für die nächste Funktion.
a)

Aufgabe 2:
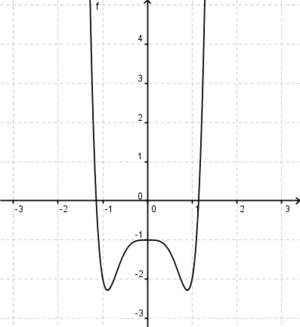
Gegeben ist die Funktion f(x)=4x6+8x5-12x4-24x3
- a) Bestimme die Definitionsmenge
- b) Berechne die Nullstellen
- c) Bestimme das Verhalten der Funktion an den Rändern des Definitionsbereichs
Aufgabe 3:
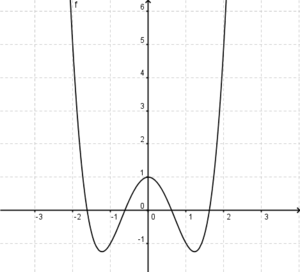
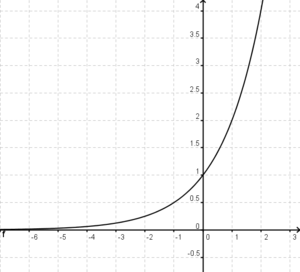
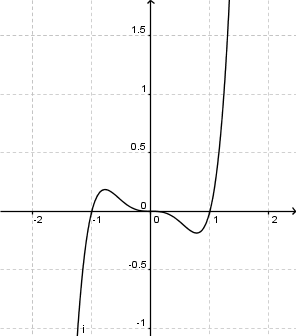
Ordne den abgebildeten Funkionen die entsprechenden Begriffe zu. (oben: Funktionstyp , unten: Symmetrie)
Ganzrationale FunktionAchsensymmetrie zu x=4Punktsymmetrie zum UrsprungGanzrationale FunktionAchsensymmetrie zur y-AchseTrigonometrische FunktionPunktsymmetrie zum UrsprungGanzrationale Funktion
Aufgabe 4:
Klicke auf die Ziffern, um das Kreuzworträtsel zu lösen.
Benutzen Sie zur Eingabe die Tastatur. Eventuell müssen sie zuerst ein Eingabefeld durch Anklicken aktivieren. - Senkrecht
- An welcher Achse wird der Graph gespiegelt? g(x)=-f(x)1
- Trigonometrische Funktion4
- Eine ungerade Funktion ist ...-symmetrisch5
- Eine Funktion, die für x→unendlich einen Grenzwert besitzt, ist ...6
- Formel zur Nullstellenbestimmung bei Quadratischen Gleichungen8
- Der Wert, dem sich ein Graph für größer werdende x-Werte annähert9
- Welche Symmetrie liegt vor? f(-x)=f(x)10
- Waagrecht
- Schnittpunkt des Graphen mit der x-Achse2
- An welcher Achse wird der Graph gespiegelt? g(x)=f(-x)3
- Eine Funktion, die keine Grenzwerte besitzt, heißt...7
Aufgabe 5:
Ordne den abgebildeten Graphen ihren Funktionsterm zu. Alle Funktionen sind aus der unten abgebildeten Funktion f(x)=x5-x3+1 entstanden.

-2[x+1]5+2[x+1]3-2-x5-x32x5-2x3-2x5-x3-1[x-2]5-[x-2]3+2
Aufgabe 6: Abschlusstest
Der folgende Multiple Choice Test ist die letzte Aufgabe des Lernpfades. Er deckt alle behandelten Themengebiete ab. Wenn du bei einigen Aufgaben nicht weiter weißt, kannst du deine Notizen zur Rate ziehen. Sollte auch das nicht helfen, solltest du dir die entsprechenden Kapitel noch einmal anschauen und deine Notizen eventuell überarbeiten. Wie immer können mehrere Antwortmöglichkeiten richtig sein.
- Du hast es geschafft!
- Du hast den ganzen Lernpfad durchgearbeitet!
- Jetzt solltest du dich mit den Eigenschaften von Funktionen und ihrer Graphen auskennen.
Zurück zur Übersicht
|



 Streckung um 0,5 in y-Richtung
Streckung um 0,5 in y-Richtung 
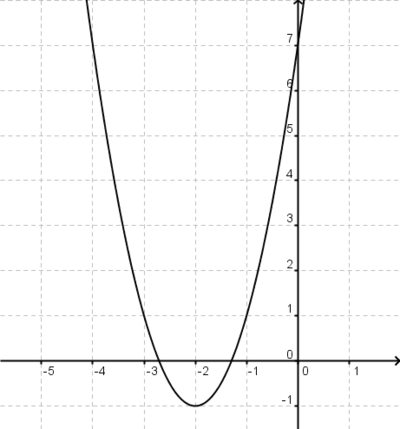
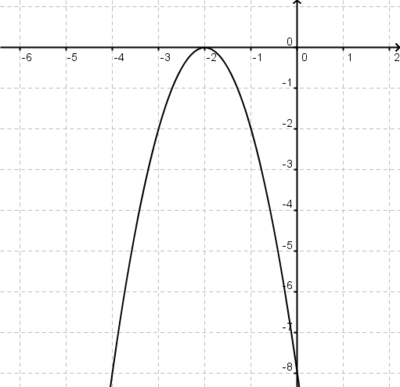


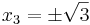
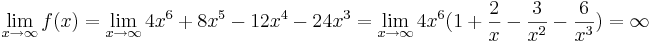
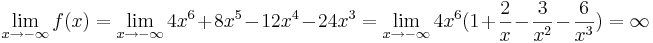
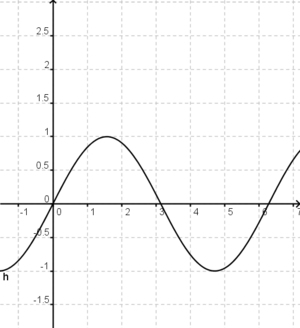







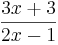 ist eine
ist eine