Übungsaufgaben: Unterschied zwischen den Versionen
(→Übungsaufgaben) |
(→Übungsaufgaben) |
||
| (2 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 54: | Zeile 54: | ||
:Ausprobieren: f(-2)=0 <math>\rightarrow</math> x<sub>2</sub>=-2 <br /> | :Ausprobieren: f(-2)=0 <math>\rightarrow</math> x<sub>2</sub>=-2 <br /> | ||
| − | :Polynomdivision: (x<sup>3</sup>+2x<sup>2</sup>-3x-6)÷(x+2)=x<sup>2</sup>-3 <math>\rightarrow</math> | + | :Polynomdivision: (x<sup>3</sup>+2x<sup>2</sup>-3x-6)÷(x+2)=x<sup>2</sup>-3 <math>\rightarrow</math> <math>x_3=\pm \sqrt 3</math> <br /> |
| − | c)<br /> <math>\lim_{x\to\infty} f(x)=\lim_{x\to\infty} | + | c)<br /> <math>\lim_{x\to\infty} f(x)=\lim_{x\to\infty}4x^6+8x^5-12x^4-24x^3=\lim_{x\to\infty}4x^6(1+ \frac {2} {x}- \frac {3} {x^2}- \frac {6} {x^3})=\infty</math> <br /> |
| − | <math>\lim_{x\to-\infty} f(x)=\lim_{x\to-\infty} | + | <math>\lim_{x\to-\infty} f(x)=\lim_{x\to-\infty}4x^6+8x^5-12x^4-24x^3=\lim_{x\to-\infty}4x^6(1+ \frac {2} {x}- \frac {3} {x^2}- \frac {6} {x^3})= \infty</math> |
</popup> | </popup> | ||
<br /> <br /> | <br /> <br /> | ||
| Zeile 111: | Zeile 111: | ||
<span style="color: blue"> '''Aufgabe 5:''' </span> <br /> | <span style="color: blue"> '''Aufgabe 5:''' </span> <br /> | ||
| − | Ordne den abgebildeten Graphen ihren Funktionsterm zu. Alle Funktionen sind aus der unten abgebildeten Funktion f(x)=x<sup>5</sup>-x<sup>3</sup>+1. <br /> <br /> | + | Ordne den abgebildeten Graphen ihren Funktionsterm zu. Alle Funktionen sind aus der unten abgebildeten Funktion f(x)=x<sup>5</sup>-x<sup>3</sup>+1 entstanden. <br /> <br /> |
[[Bild:Übungsaufgabe 6.5.1neupng|300px]] | [[Bild:Übungsaufgabe 6.5.1neupng|300px]] | ||
Aktuelle Version vom 27. Januar 2010, 21:19 Uhr
Übungsaufgaben Aufgabe 1:
Aufgabe 5:
Aufgabe 6: Abschlusstest 1.Die Funktion f(x)= 2. Eine Funktion, die keinen Grenzwert besitzt, ist (Divergent) (!Konvergent) (!Punktsymmetrisch zum Ursprung) (!Gebrochen rational) 3. Der Zusammenhang g(x)=f(-x) entspricht (!Einer Achsensymmetrie zur y-Achse) (!Einer Spiegelung an der x-Achse) (!Einer Punktsymmetrie zum Ursprung) (Einer Spiegelung an der y-Achse) (!Einer Streckung in x-Richtung) 4. Der abgebildete Graph der Funktion f(x)=x4-3x2+1 ist 5. Der Funktionsterm der Funktion g(x), die von f(x)=2x4-x3 ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet (6x4-3x3+2) (!2[3x]4-[2x]3+2) (!6x4-3x3+6) (!5x4-3x3+1) (!6[x+2]4-3[x+2]3) (!6x4-3x3) 6. 7. Der Graph der Funktion f(x)=2x2+1 ist gegenüber dem Graphen g(x)=x2-1 (!In y-Richtung Gestreckt und nach unten verschoben) (Nach oben verschoben ) (In y-Richtung gestreckt und in positiver y-Richtung verschoben ) (In y-Richtung gestreckt ) (!In negativer y-Richtung verschoben) (!Gar nicht verschoben) (!Gar nicht gestreckt) 8. Was trifft auf diese Funktion zu? f(x)=sinx (Punktsymmetrie zum Ursprung) (Trigonometrisch) (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (!Achsensymmetrie zur y-Achse) (f[0]=0) 9. Bei einer Streckung in x-Richtung (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert ) (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor 10. Um einen Graphen an der y-Achse zu spiegeln (!Multipliziert man den Funktionsterm mit -1) (Setzt man für f[x] f[-x]ein ) (Schreibt man vor jedes x ein „Minus“ ) (!Verschiebt man den Graphen nach rechts oder links [je nach Lage]) 11. Um was für eine Funktion handelt es sich? 12. 13. Wie lautet der Funktionsterm der Funktion g(x), die von f(x)=x3+x2-1 ausgehend zwei Einheiten weiter rechts verläuft? (![x+2]3+[x+2]2-1) (!x3+x2+1) ([x-2]3+[x-2]2-1) (!x3+x2-3) (x3-5x2+8x-5) (!x3+5x2-8x+5)
|
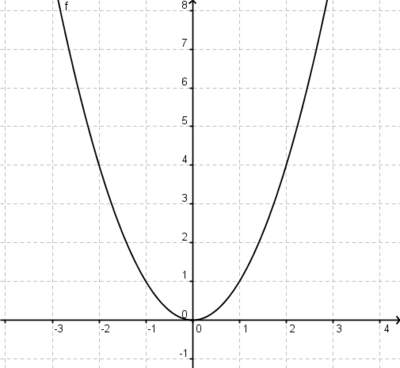
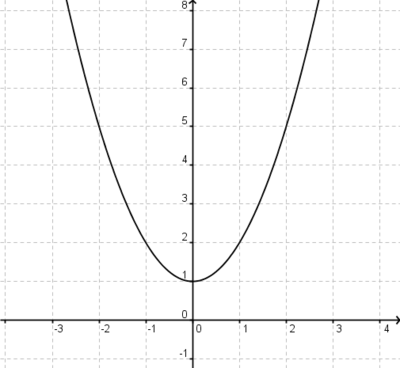
Streckung um 0,5 in y-Richtung 
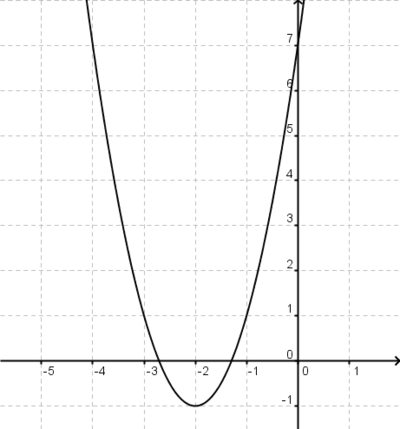
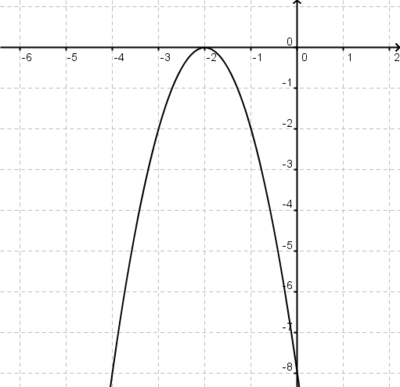
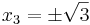
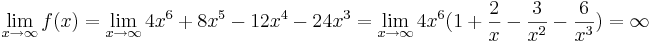
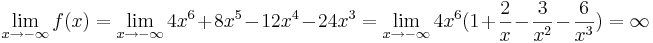
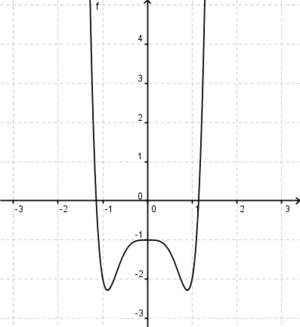
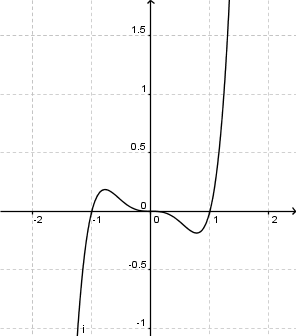
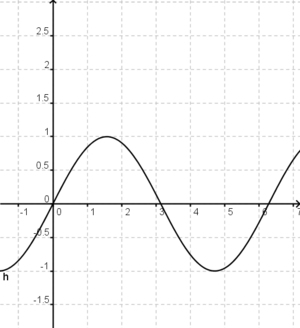
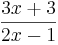ist eine (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion)
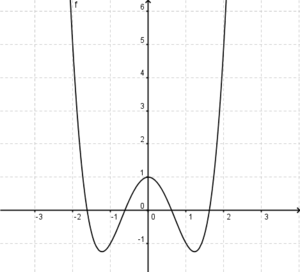
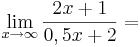(!Unendlich) (!2) (!1) (!0) (4) (!-2) (!0,5)
)
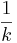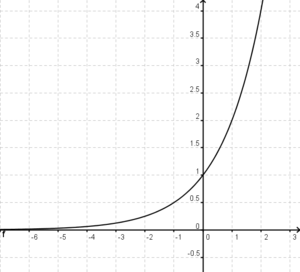
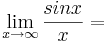(!Existiert nicht) (!Unendlich) (0)(!1)
