Übungsaufgaben: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Übungsaufgaben)
 
(5 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 54: Zeile 54:
  
 
:Ausprobieren: f(-2)=0 <math>\rightarrow</math> x<sub>2</sub>=-2 <br />
 
:Ausprobieren: f(-2)=0 <math>\rightarrow</math> x<sub>2</sub>=-2 <br />
−
:Polynomdivision: (x<sup>3</sup>+2x<sup>2</sup>-3x-6)÷(x+2)=x<sup>2</sup>-3 <math>\rightarrow</math> x<sub>3</sub>=±√3 <br />
+
:Polynomdivision: (x<sup>3</sup>+2x<sup>2</sup>-3x-6)÷(x+2)=x<sup>2</sup>-3 <math>\rightarrow</math> <math>x_3=\pm \sqrt 3</math> <br />
−
c)<br />  <math>\lim_{x\to\infty} f(x)=\lim_{x\to\infty}</math>4x<sup>6</sup>+8x<sup>5</sup>-12x<sup>4</sup>-24x<sup>3</sup>=<math>\lim_{x\to\infty}</math>4x<sup>3</sup>(x<sup>3</sup>+2x<sup>2</sup>-3x-6)=<math>\infty</math> <br />
+
c)<br />  <math>\lim_{x\to\infty} f(x)=\lim_{x\to\infty}4x^6+8x^5-12x^4-24x^3=\lim_{x\to\infty}4x^6(1+ \frac {2} {x}- \frac {3} {x^2}- \frac {6} {x^3})=\infty</math> <br />
−
<math>\lim_{x\to-\infty} f(x)=\lim_{x\to-\infty}</math>4x<sup>6</sup>+8x<sup>5</sup>-12x<sup>4</sup>-24x<sup>3</sup>=<math>\lim_{x\to-\infty}</math>4x<sup>3</sup>(x<sup>3</sup>+2x<sup>2</sup>-3x-6)=<math>\infty</math>
+
<math>\lim_{x\to-\infty} f(x)=\lim_{x\to-\infty}4x^6+8x^5-12x^4-24x^3=\lim_{x\to-\infty}4x^6(1+ \frac {2} {x}- \frac {3} {x^2}- \frac {6} {x^3})= \infty</math>
 
</popup>
 
</popup>
 
<br /> <br />
 
<br /> <br />
Zeile 111: Zeile 111:
  
 
<span style="color: blue"> '''Aufgabe 5:''' </span> <br />
 
<span style="color: blue"> '''Aufgabe 5:''' </span> <br />
−
Ordne den abgebildeten Graphen ihren Funktionsterm zu. Alle Funktionen sind aus der unten abgebildeten Funktion f(x)=x<sup>5</sup>-x<sup>3</sup>+1. <br /> <br />
+
Ordne den abgebildeten Graphen ihren Funktionsterm zu. Alle Funktionen sind aus der unten abgebildeten Funktion f(x)=x<sup>5</sup>-x<sup>3</sup>+1 entstanden. <br /> <br />
 
[[Bild:Übungsaufgabe 6.5.1neupng|300px]]
 
[[Bild:Übungsaufgabe 6.5.1neupng|300px]]
  
Zeile 146: Zeile 146:
 
'''7.  Der Graph der Funktion f(x)=2x<sup>2</sup>+1 ist gegenüber dem Graphen g(x)=x<sup>2</sup>-1 '''  (!In y-Richtung Gestreckt und nach unten verschoben) (Nach oben verschoben )  (In y-Richtung gestreckt und in positiver y-Richtung verschoben ) (In y-Richtung gestreckt ) (!In negativer y-Richtung verschoben) (!Gar nicht verschoben) (!Gar nicht gestreckt)
 
'''7.  Der Graph der Funktion f(x)=2x<sup>2</sup>+1 ist gegenüber dem Graphen g(x)=x<sup>2</sup>-1 '''  (!In y-Richtung Gestreckt und nach unten verschoben) (Nach oben verschoben )  (In y-Richtung gestreckt und in positiver y-Richtung verschoben ) (In y-Richtung gestreckt ) (!In negativer y-Richtung verschoben) (!Gar nicht verschoben) (!Gar nicht gestreckt)
  
−
'''8.  Was trifft auf diese Funktion zu? f(x)=sinx'''  (Punktsymmetrie zum Ursprung) (Trigonometrisch)  (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (Ungerade) (!Achsensymmetrie zur y-Achse) (f[0]=0)
+
'''8.  Was trifft auf diese Funktion zu? f(x)=sinx'''  (Punktsymmetrie zum Ursprung) (Trigonometrisch)  (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (!Achsensymmetrie zur y-Achse) (f[0]=0)
  
 
'''9.  Bei einer Streckung in x-Richtung '''  (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert )  (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor <math>{1 \over k}</math>)  
 
'''9.  Bei einer Streckung in x-Richtung '''  (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert )  (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor <math>{1 \over k}</math>)  
Zeile 160: Zeile 160:
  
 
</div>
 
</div>
−
 
+
<br /> <br />
−
<span style="color: blue">'''Du hast es geschafft!'''</span> <br />  
+
<big>
−
<span style="color: blue">'''Du hast den ganzen Lernpfad durchgearbeitet!'''</span>  <br />
+
:<span style="color: blue">'''Du hast es geschafft!'''</span> <br />  
−
<span style="color: blue">'''Jetzt solltest du dich mit den Eigenschaften von Funktionen und ihrer Graphen auskennen.'''</span> <br /> <br />
+
:<span style="color: blue">'''Du hast den ganzen Lernpfad durchgearbeitet!'''</span>  <br />
 +
:<span style="color: blue">'''Jetzt solltest du dich mit den Eigenschaften von Funktionen und ihrer Graphen auskennen.'''   </span> <br /> <br />
  
  
 
[[Facharbeit Florian Wilk|Zurück zur Übersicht]]
 
[[Facharbeit Florian Wilk|Zurück zur Übersicht]]

Aktuelle Version vom 27. Januar 2010, 21:19 Uhr

Übungsaufgaben

Aufgabe 1:
Beschreibe, wie die unten abgebildeten Funktionen aus den vorangegangen Funktionen entstanden sind.


Ausgangsfunktion
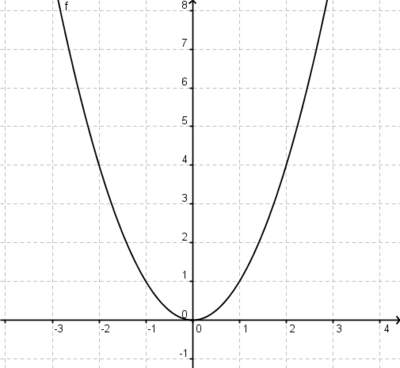
Aufgabe6.6.1neu.png
Beispiel:
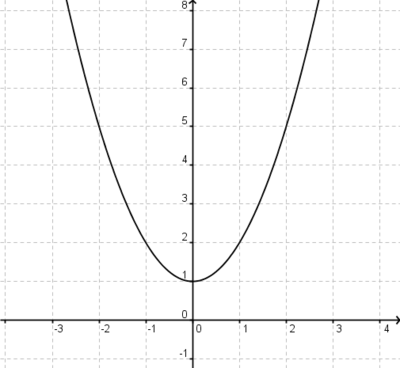
Aufgabe6.6.2neu.png
Verschiebung um 1 Einheit in positiver y-Richtung Diese Funktion dient nun als Ausgangsfunktion für die nächste Funktion.
a)


Aufgabe6.6.3neu.png



Aufgabe 2:
Gegeben ist die Funktion f(x)=4x6+8x5-12x4-24x3

a) Bestimme die Definitionsmenge
b) Berechne die Nullstellen
c) Bestimme das Verhalten der Funktion an den Rändern des Definitionsbereichs




Aufgabe 3:
Ordne den abgebildeten Funkionen die entsprechenden Begriffe zu. (oben: Funktionstyp , unten: Symmetrie)


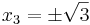
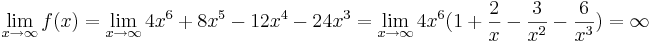
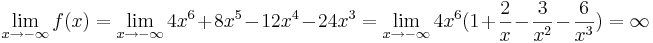
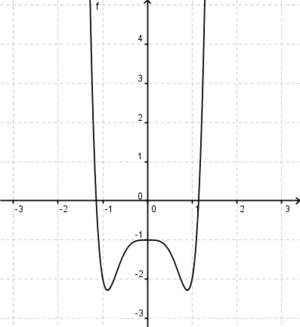
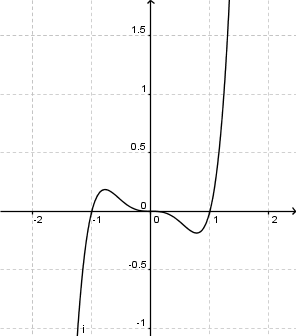
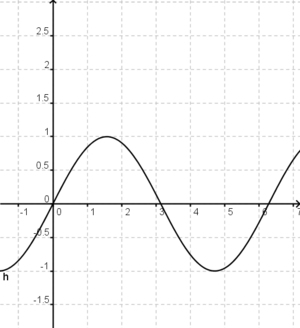
Aufgabe6.3.1neu..png Aufgabe6.3.4neu.png Aufgabe6.3.3neu.png Aufgabe6.3.2neu.png
Ganzrationale Funktion Ganzrationale Funktion Trigonometrische Funktion Ganzrationale Funktion
Achsensymmetrie zur y-Achse Punktsymmetrie zum Ursprung Punktsymmetrie zum Ursprung Achsensymmetrie zu x=4





Aufgabe 4:
Klicke auf die Ziffern, um das Kreuzworträtsel zu lösen.

Achsensymmetrie Welche Symmetrie liegt vor? f(-x)=f(x)
Grenzwert Der Wert, dem sich ein Graph für größer werdende x-Werte annähert
divergent Eine Funktion, die keine Grenzwerte besitzt, heißt...
punkt Eine ungerade Funktion ist ...-symmetrisch
konvergent Eine Funktion, die für x→unendlich einen Grenzwert besitzt, ist ...
y-Achse An welcher Achse wird der Graph gespiegelt? g(x)=f(-x)
Lösungsformel Formel zur Nullstellenbestimmung bei Quadratischen Gleichungen
Sinus Trigonometrische Funktion
Nullstelle Schnittpunkt des Graphen mit der x-Achse
x-Achse An welcher Achse wird der Graph gespiegelt? g(x)=-f(x)







Aufgabe 5:
Ordne den abgebildeten Graphen ihren Funktionsterm zu. Alle Funktionen sind aus der unten abgebildeten Funktion f(x)=x5-x3+1 entstanden.

Übungsaufgabe 6.5.1neupng


Übungsaufgabe 6.5.2neupng Übungsaufgabe 6.5.3neupng Übungsaufgabe 6.5.4neupng Übungsaufgabe 6.5.5neupng Übungsaufgabe 6.5.6neupng
x5-x3-1 [x-2]5-[x-2]3+2 2x5-2x3-2 -x5-x3 -2[x+1]5+2[x+1]3-2




Aufgabe 6: Abschlusstest
Der folgende Multiple Choice Test ist die letzte Aufgabe des Lernpfades. Er deckt alle behandelten Themengebiete ab. Wenn du bei einigen Aufgaben nicht weiter weißt, kannst du deine Notizen zur Rate ziehen. Sollte auch das nicht helfen, solltest du dir die entsprechenden Kapitel noch einmal anschauen und deine Notizen eventuell überarbeiten. Wie immer können mehrere Antwortmöglichkeiten richtig sein.

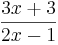1.Die Funktion f(x)={3x+3 \over2x-1} ist eine (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion)

2. Eine Funktion, die keinen Grenzwert besitzt, ist (Divergent) (!Konvergent) (!Punktsymmetrisch zum Ursprung) (!Gebrochen rational)

3. Der Zusammenhang g(x)=f(-x) entspricht (!Einer Achsensymmetrie zur y-Achse) (!Einer Spiegelung an der x-Achse) (!Einer Punktsymmetrie zum Ursprung) (Einer Spiegelung an der y-Achse) (!Einer Streckung in x-Richtung)

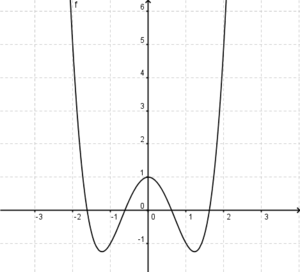
4. Der abgebildete Graph der Funktion f(x)=x4-3x2+1 ist Abschlusstest2neu.png (!Punktsymmetrisch zum Ursprung) (Gerade) (Ganzrational) (!Quadratisch) (Achsensymmetrisch zur y-Achse) (!Ungerade) (Divergent) (!Konvergent)

5. Der Funktionsterm der Funktion g(x), die von f(x)=2x4-x3 ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet (6x4-3x3+2) (!2[3x]4-[2x]3+2) (!6x4-3x3+6) (!5x4-3x3+1) (!6[x+2]4-3[x+2]3) (!6x4-3x3)

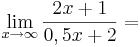6. \lim_{x\to\infty} {2x+1 \over 0,5x+2}= (!Unendlich) (!2) (!1) (!0) (4) (!-2) (!0,5)

7. Der Graph der Funktion f(x)=2x2+1 ist gegenüber dem Graphen g(x)=x2-1 (!In y-Richtung Gestreckt und nach unten verschoben) (Nach oben verschoben ) (In y-Richtung gestreckt und in positiver y-Richtung verschoben ) (In y-Richtung gestreckt ) (!In negativer y-Richtung verschoben) (!Gar nicht verschoben) (!Gar nicht gestreckt)

8. Was trifft auf diese Funktion zu? f(x)=sinx (Punktsymmetrie zum Ursprung) (Trigonometrisch) (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (!Achsensymmetrie zur y-Achse) (f[0]=0)

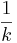9. Bei einer Streckung in x-Richtung (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert ) (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor {1 \over k})

10. Um einen Graphen an der y-Achse zu spiegeln (!Multipliziert man den Funktionsterm mit -1) (Setzt man für f[x] f[-x]ein ) (Schreibt man vor jedes x ein „Minus“ ) (!Verschiebt man den Graphen nach rechts oder links [je nach Lage])

11. Um was für eine Funktion handelt es sich? Abschlusstest1neu.png (Exponentialfunktion) (!Lineare Funktion ) (!Trigonometrische Funktion) (!Gebrochen rationale Funktion)

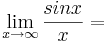12. \lim_{x\to\infty} {sinx \over x}= (!Existiert nicht) (!Unendlich) (0)(!1)

13. Wie lautet der Funktionsterm der Funktion g(x), die von f(x)=x3+x2-1 ausgehend zwei Einheiten weiter rechts verläuft? (![x+2]3+[x+2]2-1) (!x3+x2+1) ([x-2]3+[x-2]2-1) (!x3+x2-3) (x3-5x2+8x-5) (!x3+5x2-8x+5)




Du hast es geschafft!
Du hast den ganzen Lernpfad durchgearbeitet!
Jetzt solltest du dich mit den Eigenschaften von Funktionen und ihrer Graphen auskennen.


Zurück zur Übersicht

Von „http://rmg.zum.de/index.php?title=Facharbeit_Florian_Wilk/Übungsaufgaben&oldid=28491“