Strecken und Spiegeln von Funktionsgraphen: Unterschied zwischen den Versionen
(→Spiegelung an der y-Achse) |
|||
| (20 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 12: | Zeile 12: | ||
| valign="top" | | | valign="top" | | ||
''' <span style="color: blue">Zur Erinnerung:</span>''' <br /> | ''' <span style="color: blue">Zur Erinnerung:</span>''' <br /> | ||
| − | Bei quadratischen Funktionen | + | Bei quadratischen Funktionen habt ihr in der neunten Klasse bereits gelernt, dass der Funktionsgraph durch einen Koeffizienten a weiter oder enger als die Normalparabel |
f(x)=x<sup>2</sup> sein kann. Diese Erscheinung wird nun allgemein für alle Funktionstypen untersucht. | f(x)=x<sup>2</sup> sein kann. Diese Erscheinung wird nun allgemein für alle Funktionstypen untersucht. | ||
| Zeile 22: | Zeile 22: | ||
| valign="top" | | | valign="top" | | ||
''' <span style="color: blue">Problemstellung:</span>''' <br /> | ''' <span style="color: blue">Problemstellung:</span>''' <br /> | ||
| − | Im | + | {| |
| + | ! width="300" | | ||
| + | ! width="10" | | ||
| + | |- | ||
| + | | valign="top" | | ||
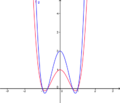
| + | <br /> <br /> Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)= 2x<sup>4</sup>-3x<sup>2</sup>+0,5 dargestellt. Wird diese Funktion nun mit einer rationalen Zahl k multipliziert, entsteht ein veränderter Graph g. Versuche, durch Verschieben des Reglers das Verhalten des Funktionsgraphen zu erklären. | ||
|} <br /> <br /> | |} <br /> <br /> | ||
| − | <ggb_applet width=" | + | | |
| + | | valign="top" | | ||
| + | <ggb_applet width="596" height="502" version="3.2" ggbBase64="UEsDBBQACAAIAMGLNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1stVZNj9s2ED03v4LgabdBZH3Y3jUgbdCmCBBg2x6cpkAPBShpLLGmSIGkvHJ+fYek5LXdFNgi6WUpDofDN29mnjd/O3aCHEAbrmRBkyimBGSlai6bgg529+aevn14lTegGig1IzulO2YLmkUpdfaBP7z6LjeteiJMeJdPHJ4KumPCACWm18Bq0wLYCzsbRi4408dfy7+gsub5IAT5IPsBX7F6QFvV1Y/czNuFf7AX3P7ED7wGTYSqCrpeIXT8+gTa8oqJgi7jYEkLml4doilzp63S/LOS1rk/B9+hhRDDPwMysna2fOETzWGoBK85ky4ZjwOdCHnitW0LutqsMSTwpkWsK4zvo1VK6Xp7NBY6Mv4BWiGc5doRfQy7LL1zO4O43INxFmXLdLNZJetNfJ8m6DcdrdJouUnv7+7mv+EBOGzBWiyYIWwEM7PWaF6ff38wPypRn4juFZf2HevtoH2ts8m0tUf3FgLSLpEfZCNgsqVYihaqfanGbSAnC6E/Hnt/xcMpm3dKKE20o32FDtNahtX7OJwnr9j7xN5jiuGCns6TTeo9/FqG1XsJLgO0Ke9sTjqJ52e4Ic7g6MUWnekQrASsOCWD5PZx3mBn7KdMk+D/y9CVOBrnvXEKmXyjkPniqqnyPWgJIrSOxLoOajDk4Fo0lM7jqKHiHW7DwUQIc8X6DQEEaw2Nhhl3mKtAlz+9aM8rc76YQTgMBrFWFgUC87Eul63V2AYgyQFt7we5d4em0axvQbrhtjhYBX2PBcS0yO9c7CmpmcWrTjRgRFUwTnECbQQzQ9kZe1xvxltSkDSKyfdk/PNmGcW35A3J5n3q9q9JHPlGykFABzis1jfgbpAe5qkaO3rZJrbFekh8GsWBTpcmGryCKS9GVyV9rj0e/0vTomz1LcOvaAon2BGF6ZxnH+1nVV+yzyRW0VOL+tC7AK5PeoB6EuMZJOkxpB/UsyZ4QWbYXoGjf7Alhw40r0557j1ZCG6YIKbRN+YmeSE3k58RXt07LgOxpGMjiqD7YqVRYrCwrbDB5aOqPIczuEmOk9jfwjvL1dLrLUqEl9odH+FZCb/8I/BFbtOrrvma8l1U5moiCtpMA9GEgdhj+9+8YCpuKXnBXDT/31zMkv/Vk/Efe3txrlP+B3v6j+Xhb1BLBwjR4fgTYQMAAOMIAABQSwECFAAUAAgACADBizc80eH4E2EDAADjCAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAJsDAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> <br /> <br /> | ||
| + | |} | ||
{| | {| | ||
| Zeile 31: | Zeile 39: | ||
| valign="top" | | | valign="top" | | ||
''' <span style="color: blue">Erklärung:</span>''' <br /> | ''' <span style="color: blue">Erklärung:</span>''' <br /> | ||
| − | Da der Graph von g(x) aus einer Multiplikation von einem Koeffizienten k und dem Funktionswert von f(x) entsteht, gilt für den Graphen g die Funktionsgleichung g(x)= | + | Da der Graph von g(x) aus einer Multiplikation von einem Koeffizienten k und dem Funktionswert von f(x) entsteht, gilt für den Graphen g die Funktionsgleichung g(x)=k<math>\cdot</math>f(x). Dadurch nimmt g bei einem Koeffizienten k>1 einen größeren Funktionswert an als der Graph von f. Der Graph ist also in y-Richtung gestreckt. Dasselbe gilt auch für 0<k<1, nur dass der Graph g hier kleinere Funktionswerte annimmt. '''Die Nullstellen bleiben dabei unverändert!''' |
|} <br /> <br /> <br /> | |} <br /> <br /> <br /> | ||
| Zeile 41: | Zeile 49: | ||
:<span style="color: green">k=3</span> <br /> | :<span style="color: green">k=3</span> <br /> | ||
:<span style="color: red">f(1)=-0,5</span> <br /> | :<span style="color: red">f(1)=-0,5</span> <br /> | ||
| − | ::g(x)=f(x)<math>\ | + | ::g(x)=f(x)<math>\cdot</math>k <br /> |
| − | ::g(1)=<span style="color: red">f(1)</span><span style="color: green"><math>\ | + | ::g(1)=<span style="color: red">f(1)</span><span style="color: green"><math>\cdot</math>3</span> <br /> |
| − | ::g(1)=-0,5<math>\ | + | ::g(1)=-0,5<math>\cdot</math>3 <br /> |
::g(1)=-1,5 </div> | ::g(1)=-1,5 </div> | ||
|} <br /> <br /> <br /> <br /> | |} <br /> <br /> <br /> <br /> | ||
| Zeile 54: | Zeile 62: | ||
|- | |- | ||
| valign="top" | | | valign="top" | | ||
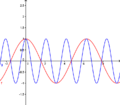
| − | Im | + | Im untenstehenden Applet ist der Graph der Funktion f(x)=cosx eingezeichnet. Durch eine Streckung in x-Richtung entsteht der Graph g. Durch Verschieben des Reglers kannst du diese Streckung beobachten. Überlege dir, welche Auswirkungen eine Streckung um den Faktor 3 auf den Funktionsgraph hat. |
|} <br /> | |} <br /> | ||
| − | <ggb_applet width=" | + | <ggb_applet width="819" height="442" version="3.2" ggbBase64="UEsDBBQACAAIAEaMNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1stVZNb9QwED3TX2H5BEjsbvarWylpBUWVkAocForEzUlmE7OOHdnONttfz9hO9osiFSiX2h6PJ2/evJltfNVWgmxAG65kQqPBiBKQmcq5LBLa2NWbBb26PIsLUAWkmpGV0hWzCZ0MxtTZG3559iI2pbonTHiXOw73CV0xYYASU2tguSkB7JGdNS0XnOnt5/QHZNbsL0KQD7Ju8CtWN2jLqvyWm/449B+sBbfv+YbnoIlQWULnM4SOuzvQlmdMJHQ6CpZxQscnl2iauNtSaf6gpHXu++ArtBBi+AMgI3Nni4c+0RiaTPCcM+mS8TjQiZB7ntsyoYvoAkMCL0rEOp2OQrRMKZ0vt8ZCRdrvoFVCZ2PH8zYcxudzdzIIC9xpcB5Nx4tZ/3eGjt1dNFoMuqCwWYK1WCRDWAumZ6rQPD/cfzDvlMh35NaKS3vNattoX99JZ1rarYuPKLQD/1YWAjpbhPSXkK1T1S4DIZMQ+su29k88nLS4VkJpoh3ViLjo1jSs3sfh3HmNvM/Ie3QxXNDdfXQx9h5+TcPqvQSXAVqX96RPOhr1n+GGOIPjFGXZ0yFYClhlShrJ7W1/QDWs95k6/09NlWI7HOphFzJ6ppDx8ERI8Rq0BBHkIrGujWoM2ThZhtJ5HDlkvMJjuOgIYa5YXxFAsOZQaOhxh14KdPnbI0memONhD8JhMIg1szgUMB/rcllajTIASTZou2nk2l2aQrO6BOka2mIzJfQGC4hpkW9crCnJmcWnblBAi5PAuCkTaCOYGY6atsb1ZfuKJCRTBjceCQioAHvQeo2tGumR7Ahf0WMl2BIplxgdu452j7pM/WBSfsacVG1fXrz+jS5xGtUlw13fdoJtcd4cUumjfVT5McFMYqE8e9j2tQvgpFAD5N2M7UGSGkP6Xjyo8xMyQwUFjn5hSzYVaJ7t8lx7shBc00GcDJ6Zm+iJ3HR+RvihXXEZiCUVa3Ekuh1LjRKNhWWGGpa3KvMc9uC6KRuN/Ct8Mz/3r7ZIjkuKrHgL+2H3+Gx/lNvxiWr+pXxHlTkRfUKLTvPFXvMYkAzJmrwmqH7yBPkX/0/+/fAORZ5Ff98Bf6jh4eHI8b+33T8clz8BUEsHCJ9famg/AwAAoggAAFBLAQIUABQACAAIAEaMNzyfX2poPwMAAKIIAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAeQMAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> <br /> <br /> |
{| | {| | ||
| Zeile 64: | Zeile 72: | ||
''' <span style="color: blue">Erklärung:</span>''' <br /> | ''' <span style="color: blue">Erklärung:</span>''' <br /> | ||
Eine Streckung um den Faktor 3 in x-Richtung bedeutet, dass der Graph von g den Funktionswert, den der Graph von f an der Stelle x annimmt, erst an der Stelle 3x annimmt. <br /> | Eine Streckung um den Faktor 3 in x-Richtung bedeutet, dass der Graph von g den Funktionswert, den der Graph von f an der Stelle x annimmt, erst an der Stelle 3x annimmt. <br /> | ||
| − | Es entsteht also der Zusammenhang f(x)=g(3x) oder g(x)=f( | + | Es entsteht also der Zusammenhang f(x)=g(3x) oder <math>g(x)=f \left( \frac {1} {3}x \right)=cos \frac {1} {3}x</math> <br /> |
| − | + | |} <br /> <br /> <br /> | |
| − | |} <br /> <br /> <br /> | + | |
{| | {| | ||
| Zeile 73: | Zeile 80: | ||
| valign="top" | | | valign="top" | | ||
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> ''' <span style="color: blue">Beispiel:</span>''' <br /> | <div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> ''' <span style="color: blue">Beispiel:</span>''' <br /> | ||
| − | :k= | + | :<span style="color: green">k=3</span> <br /> |
:f(<math>\Pi</math>)=-1 <br /> | :f(<math>\Pi</math>)=-1 <br /> | ||
| − | ::g(x)=f( | + | ::<math>g(x)=f\left( \frac {1} {k} \right)</math> <br /> |
| − | :: | + | ::<math>g(\Pi)=f \left( \frac {1} {3} \Pi \right)</math> <br /> |
| − | ::g(<math>\Pi</math>)=0 | + | ::g(<math>\Pi</math>)=0,5 |
</div> | </div> | ||
|} <br /> <br /> | |} <br /> <br /> | ||
| + | |||
{| | {| | ||
| Zeile 88: | Zeile 96: | ||
Der Zusammenhang lautet also f(x)=g(0,5x) oder g(x)=f(2x). Das Verhalten des Graphen kannst du beobachten, wenn du im oben abgebildeten Koordinatensystem den Regler k verschiebst. | Der Zusammenhang lautet also f(x)=g(0,5x) oder g(x)=f(2x). Das Verhalten des Graphen kannst du beobachten, wenn du im oben abgebildeten Koordinatensystem den Regler k verschiebst. | ||
'''Der Funktionswert an der Stelle x=0 bleibt immer gleich.''' <br /> | '''Der Funktionswert an der Stelle x=0 bleibt immer gleich.''' <br /> | ||
| − | Allgemein: g(x)=f(kx) mit dem Streckungsfaktor <math>{1 \over k}</math> | + | '''Allgemein: g(x)=f(kx)''' mit dem Streckungsfaktor <math>{1 \over k}</math> |
|} <br /> <br /> | |} <br /> <br /> | ||
| Zeile 95: | Zeile 103: | ||
|- | |- | ||
| valign="top" | | | valign="top" | | ||
| − | <div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "> | + | <div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "> <span style="color: red">'''Merke:''' </span> |
| − | Besteht zwischen zwei Funktionen der Zusammenhang g(x)= | + | Besteht zwischen zwei Funktionen der Zusammenhang g(x)=k<math>\cdot</math>f(x) mit k>0, dann ist der Graph von g gegenüber dem von f in y-Richtung um den Faktor k gestreckt. |
Besteht zwischen zwei Funktionen der Zusammenhang g(x)=f(kx) mit k>0, dann ist der Graph von g gegenüber dem von f um den Faktor <math>{1 \over k}</math> in x-Richtung gestreckt.</div> | Besteht zwischen zwei Funktionen der Zusammenhang g(x)=f(kx) mit k>0, dann ist der Graph von g gegenüber dem von f um den Faktor <math>{1 \over k}</math> in x-Richtung gestreckt.</div> | ||
|} <br /> <br /> | |} <br /> <br /> | ||
| Zeile 104: | Zeile 112: | ||
Bisher haben wir das Verhalten der Funktionsgraphen nur für positive Werte von k untersucht. Nun soll k den Wert -1 annehmen. Aus den oben erstellten <br /> | Bisher haben wir das Verhalten der Funktionsgraphen nur für positive Werte von k untersucht. Nun soll k den Wert -1 annehmen. Aus den oben erstellten <br /> | ||
Formeln ergeben sich nun die Fälle | Formeln ergeben sich nun die Fälle | ||
| − | g(x)= - | + | g(x)= -1k<math>\cdot</math>f(x) und g(x)=f(-1kx), <br /> |
| − | Zunächst betrachten wir den Fall g(x)= -f(x). <br /> | + | also g(x)= -f(x) und g(x)=f(-x). <br /> |
| + | Zunächst betrachten wir den Fall <span style="color: blue">g(x)= -f(x)</span> . <br /> | ||
{| | {| | ||
| Zeile 113: | Zeile 122: | ||
|- | |- | ||
| valign="top" | | | valign="top" | | ||
| − | [[Bild:Spiegelung an der x-Achse.png|450px|left]] | + | [[Bild:Spiegelung an der x-Achse neu.png|450px|left]] |
| | | | ||
| Zeile 123: | Zeile 132: | ||
== <span style="color: blue">Spiegelung an der y-Achse</span> == | == <span style="color: blue">Spiegelung an der y-Achse</span> == | ||
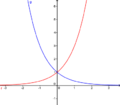
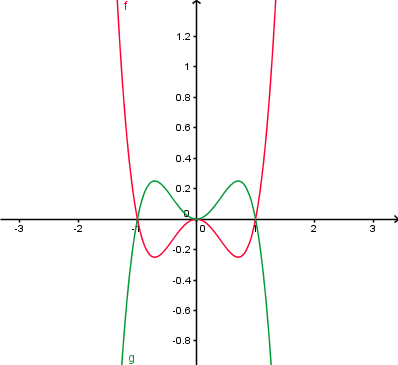
| − | Nun betrachten wir den Fall g(x)=f(-x) am Beispiel f(x)=2<sup>x</sup>. <br /> | + | Nun betrachten wir den Fall <span style="color: blue">g(x)=f(-x)</span> am Beispiel f(x)=2<sup>x</sup>. <br /> |
{| | {| | ||
| Zeile 131: | Zeile 140: | ||
|- | |- | ||
| valign="top" | | | valign="top" | | ||
| − | [[Bild:Spiegelung an der y-Achse.png|450px|left]] | + | [[Bild:Spiegelung an der y-Achse neu.png|450px|left]] |
| | | | ||
| valign="top" | | | valign="top" | | ||
| Zeile 143: | Zeile 152: | ||
|- | |- | ||
| − | <div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "> | + | <div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "><span style="color: red">'''Merke:''' </span> <br /> |
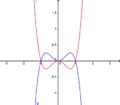
| − | Der Graph von g mit '''g(x)= -f(x)''' geht aus dem Graphen von f durch eine '''Spiegelung an der x-Achse''' hervor. <br /> | + | Der Graph von g mit '''g(x)=-f(x)''' geht aus dem Graphen von f durch eine '''Spiegelung an der x-Achse''' hervor. <br /> |
Der Graph von g mit '''g(x)=f(-x)''' geht aus dem Graphen von f durch eine '''Spiegelung an der y-Achse''' hervor. <br /> <br /> | Der Graph von g mit '''g(x)=f(-x)''' geht aus dem Graphen von f durch eine '''Spiegelung an der y-Achse''' hervor. <br /> <br /> | ||
| Zeile 156: | Zeile 165: | ||
== <span style="color: blue">Beispielaufgaben</span> == | == <span style="color: blue">Beispielaufgaben</span> == | ||
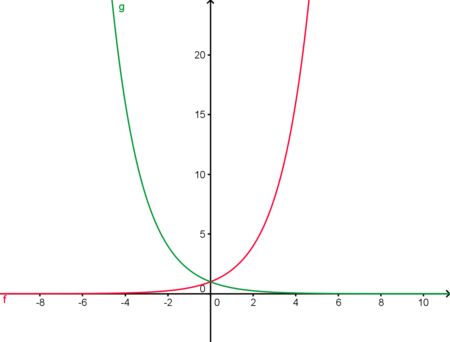
| − | ''' <span style="color: blue">Aufgabe 1:</span>''' <br /> | + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 1:</span>''' <br /> |
| − | Zeichne in ein gemeinsames Koordinatensystem die Funktion f(x)=x<sup>3</sup>+2, sowie die Funktionen g(x)=2f(x) und h(x)=f(2x). <br /> <br /> | + | Zeichne in ein gemeinsames Koordinatensystem die Funktion f(x)=x<sup>3</sup>+2, sowie die Funktionen g(x)=2f(x) und h(x)=f(2x) (handschriftlich). <br /> <br /> |
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | [[Bild:Lösung Strekungsaufgabe 1.png|600px]] | + | [[Bild:Lösung Strekungsaufgabe 2.1.png|600px]] |
| − | </popup> <br /> | + | </popup> </div> <br /> |
| − | ''' <span style="color: blue">Aufgabe 2:</span>''' <br /> | + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 2:</span>''' <br /> |
Gegeben ist die Funktion f(x)=2x<sup>3</sup>-x<sup>2</sup>+2x+1. Erstelle jeweils die neuen Funktionen nach den folgenden Anweisungen. Verwende zum Weiterrechnen jeweils den vorangegangenen Funktionsterm.<br /> | Gegeben ist die Funktion f(x)=2x<sup>3</sup>-x<sup>2</sup>+2x+1. Erstelle jeweils die neuen Funktionen nach den folgenden Anweisungen. Verwende zum Weiterrechnen jeweils den vorangegangenen Funktionsterm.<br /> | ||
:a) Streckung um den Faktor 3 in y-Richtung <br /> | :a) Streckung um den Faktor 3 in y-Richtung <br /> | ||
| Zeile 172: | Zeile 181: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
f(x)=2x<sup>3</sup>-x<sup>2</sup>+2x+1 <br /> <br /> | f(x)=2x<sup>3</sup>-x<sup>2</sup>+2x+1 <br /> <br /> | ||
| − | a) Streckung um den Faktor 3 in y-Richtung <br /> | + | a) Streckung um den Faktor <span style="color: red">3 in y-Richtung</span> <br /> |
| − | ::g(x)=k<math>\ | + | ::g(x)=<span style="color: red">k</span><math>\cdot</math>f(x) mit <span style="color: red">k=3</span> <br /> |
| − | ::g(x)=3<math>\ | + | ::g(x)=<span style="color: red">3</span><math>\cdot</math>(2x<sup>3</sup>-x<sup>2</sup>+2x+1) <br /> |
::g(x)=6x<sup>3</sup>-3x<sup>2</sup>+6x+3 <br /> <br /> | ::g(x)=6x<sup>3</sup>-3x<sup>2</sup>+6x+3 <br /> <br /> | ||
| − | b) Spiegelung an der x-Achse <br /> | + | b) <span style="color: red">Spiegelung an der x-Achse</span> <br /> |
| − | ::h(x)=-g(x) <br /> | + | ::<span style="color: red">h(x)=-g(x)</span> <br /> |
::h(x)=-(6x<sup>3</sup>-3x<sup>2</sup>+6x+3) <br /> | ::h(x)=-(6x<sup>3</sup>-3x<sup>2</sup>+6x+3) <br /> | ||
::h(x)=-6x<sup>3</sup>+3x<sup>2</sup>-6x-3 <br /> <br /> | ::h(x)=-6x<sup>3</sup>+3x<sup>2</sup>-6x-3 <br /> <br /> | ||
| − | c) Streckung um den Faktor 0,5 in x-Richtung <br /> | + | c) Streckung um den Faktor <span style="color: red">0,5 in x-Richtung</span> <br /> |
| − | ::i(x)=h(kx) mit k=<math>{1 \over 0,5}</math>=2 <br /> | + | ::<span style="color: red">i(x)=h(kx)</span> mit <span style="color: red">k=</span><math>{1 \over 0,5}</math>=<span style="color: red">2</span> <br /> |
| − | ::i(x)=h(2x) <br /> | + | ::i(x)=h(<span style="color: red">2x</span>) <br /> |
::i(x)=-6(2x)<sup>3</sup>+3(2x)<sup>2</sup>-6(2x)-3 <br /> | ::i(x)=-6(2x)<sup>3</sup>+3(2x)<sup>2</sup>-6(2x)-3 <br /> | ||
::i(x)=-48x<sup>3</sup>+12x<sup>2</sup>-12x-3 <br /> <br /> | ::i(x)=-48x<sup>3</sup>+12x<sup>2</sup>-12x-3 <br /> <br /> | ||
| − | d) Streckung um den Faktor 0,25 in y-Richtung <br /> | + | d) Streckung um den Faktor <span style="color: red">0,25 in y-Richtung</span> <br /> |
| − | ::k(x)=0,25<math>\ | + | ::k(x)=<span style="color: red">0,25</span><math>\cdot</math>i(x) <br /> |
::k(x)=-12x<sup>3</sup>+3x<sup>2</sup>-3x-0,75 <br /> <br /> | ::k(x)=-12x<sup>3</sup>+3x<sup>2</sup>-3x-0,75 <br /> <br /> | ||
| − | e) Spiegelung an der y-Achse <br /> | + | e) <span style="color: red">Spiegelung an der y-Achse</span> <br /> |
| − | ::l(x)=k(-x)<br /> | + | ::<span style="color: red">l(x)=k(-x)</span> <br /> |
::l(x)=-12(-x<sup>3</sup> )+3(-x<sup>2</sup> )-3(-x)-0,75 <br /> | ::l(x)=-12(-x<sup>3</sup> )+3(-x<sup>2</sup> )-3(-x)-0,75 <br /> | ||
::l(x)=12x<sup>3</sup>-3x<sup>2</sup>+3x-0,75 <br /> <br /> | ::l(x)=12x<sup>3</sup>-3x<sup>2</sup>+3x-0,75 <br /> <br /> | ||
| − | </popup> | + | </popup> </div> |
| Zeile 205: | Zeile 214: | ||
{| | {| | ||
|- | |- | ||
| − | | <big> '''Spiegelung an der x-Achse'''</big> || [[Bild:Memory | + | | <big> '''Spiegelung an der x-Achse'''</big> || [[Bild:Memory Streckung1neu.png|120px]] |
|- | |- | ||
| − | | <big> '''Spiegelung an der y-Achse'''</big> || [[Bild:Memory | + | | <big> '''Spiegelung an der y-Achse'''</big> || [[Bild:Memory Streckung2neu.png|120px]] |
|- | |- | ||
| − | | <big> '''Streckung in x-Richtung'''</big> || [[Bild:Memory | + | | <big> '''Streckung in x-Richtung'''</big> || [[Bild:Memory Streckung3neu.png|120px]] |
|- | |- | ||
| − | | <big> '''Streckung in y-Richtung'''</big> || [[Bild:Memory | + | | <big> '''Streckung in y-Richtung'''</big> || [[Bild:Memory Streckung4neu.png|120px]] |
| − | + | ||
| − | |||
|} | |} | ||
| + | </div> <br /> | ||
| + | |} | ||
| + | |||
Aktuelle Version vom 27. Januar 2010, 20:07 Uhr
Strecken und Spiegeln von FunktionsgraphenStreckung in y-Richtung
Streckung in x-Richtung Problemstellung:
Spiegelung an der x-AchseBisher haben wir das Verhalten der Funktionsgraphen nur für positive Werte von k untersucht. Nun soll k den Wert -1 annehmen. Aus den oben erstellten
Spiegelung an der y-AchseNun betrachten wir den Fall g(x)=f(-x) am Beispiel f(x)=2x.
Wie sich der Graph einer Funktion verhält, wenn er an der x-Achse gespiegelt und dann in y-Richtung gestreckt wird, kannst du im untenstehenden Applet beobachten.
Beispielaufgaben Aufgabe 1: Zeichne in ein gemeinsames Koordinatensystem die Funktion f(x)=x3+2, sowie die Funktionen g(x)=2f(x) und h(x)=f(2x) (handschriftlich). Aufgabe 2:
Gegeben ist die Funktion f(x)=2x3-x2+2x+1. Erstelle jeweils die neuen Funktionen nach den folgenden Anweisungen. Verwende zum Weiterrechnen jeweils den vorangegangenen Funktionsterm.
|
 f(x). Dadurch nimmt g bei einem Koeffizienten k>1 einen größeren Funktionswert an als der Graph von f. Der Graph ist also in y-Richtung gestreckt. Dasselbe gilt auch für 0<k<1, nur dass der Graph g hier kleinere Funktionswerte annimmt. Die Nullstellen bleiben dabei unverändert!
f(x). Dadurch nimmt g bei einem Koeffizienten k>1 einen größeren Funktionswert an als der Graph von f. Der Graph ist also in y-Richtung gestreckt. Dasselbe gilt auch für 0<k<1, nur dass der Graph g hier kleinere Funktionswerte annimmt. Die Nullstellen bleiben dabei unverändert!
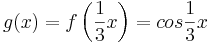
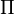 )=-1
)=-1 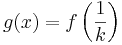
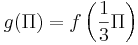
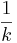
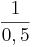 =
=