Symmetrie von Funktionsgraphen: Unterschied zwischen den Versionen
(→Punktsymmetrie zum Ursprung) |
(→Beispielaufgaben) |
||
| (16 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| + | {| | ||
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
= <span style="color: blue">Symmetrie von Funktionsgraphen</span> = | = <span style="color: blue">Symmetrie von Funktionsgraphen</span> = | ||
== <span style="color: blue">Achsensymmetrie</span> == | == <span style="color: blue">Achsensymmetrie</span> == | ||
| Zeile 6: | Zeile 10: | ||
|- | |- | ||
| valign="top" | | | valign="top" | | ||
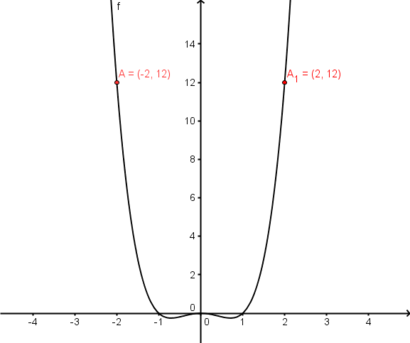
| − | Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=x<sup> | + | Im nebenstehenden Koordinatensystem ist der Graph der Funktion <br /> |
| + | f(x)=x<sup>4</sup>-x<sup>2</sup> abgebildet. Bei der Betrachtung des Graphen fällt auf, dass er auf beiden Seiten der y-Achse den gleichen Verlauf nimmt. Wenn man also einen Punkt des Graphen an der y-Achse spiegelt, liegt der Spiegelpunkt ebenfalls auf dem Graphen. Dies wird als <span style="color: blue">'''Achsensymmetrie zur y-Achse'''</span> bezeichnet. Zum Beweis dieser Symmetrie nutzt man den Zusammenhang <span style="color: blue">'''f(x)=f(-x)'''</span>. Wenn also das Einsetzen von f(x) und f(-x) den gleichen Funktionswert ergibt, handelt es sich um einen <span style="color: blue">'''achsensymmetrischen Graphen'''</span>. | ||
| − | Setzt man beispielsweise in diesem Fall | + | Setzt man beispielsweise in diesem Fall 2 und -2 in den Funktionsterm ein, so kommt beide Male das gleiche Ergebnis dabei heraus: <br /> |
| − | ::f( | + | ::f(2)=2<sup>4</sup>-2<sup>2</sup>=12 <br /> |
| − | ::f(- | + | ::f(-2)=(-2)<sup>4</sup>-(-2)<sup>2</sup>=12 <br /> <br /> |
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> | <div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> | ||
In der Regel wird dieser Beweis allerdings allgemein durchgeführt, indem man –x in den Funktionsterm einsetzt: <br /> | In der Regel wird dieser Beweis allerdings allgemein durchgeführt, indem man –x in den Funktionsterm einsetzt: <br /> | ||
| − | ::f(x)=x<sup> | + | ::f(x)=x<sup>4</sup>-x<sup>2</sup> <br /> |
| − | ::<span style="color: blue">'''f(-x)'''</span>=(-x)<sup> | + | ::<span style="color: blue">'''f(-x)'''</span>=(-x)<sup>4</sup>-(-x)<sup>2</sup> <br /> |
| − | :: =x<sup> | + | :: =x<sup>4</sup>-x<sup>2</sup> <br /> |
:: <span style="color: blue">'''=f(x)'''</span> </div> <br /> <br /> <br /> <br /> | :: <span style="color: blue">'''=f(x)'''</span> </div> <br /> <br /> <br /> <br /> | ||
| | | | ||
| valign="top" | | | valign="top" | | ||
| − | [[Bild:Graph Achsensymmetrie.png|410px]] | + | [[Bild:Graph Achsensymmetrie neu.png|410px]] |
|} | |} | ||
== <span style="color: blue">Punktsymmetrie zum Ursprung</span> == | == <span style="color: blue">Punktsymmetrie zum Ursprung</span> == | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
{| | {| | ||
! width="500" | | ! width="500" | | ||
| − | ! width=" | + | ! width="100" | |
|- | |- | ||
| valign="top" | | | valign="top" | | ||
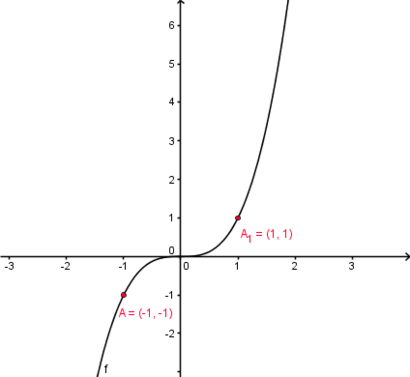
| − | Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=x<sup>3</sup> dargestellt. Hier lässt sich nicht wie im vorigen Fall eine Symmetrie zu einer Achse feststellen. Stattdessen ist diese Funktion symmetrisch zum Ursprung | + | Im nebenstehenden Koordinatensystem ist der Graph der Funktion <br /> |
| + | f(x)=x<sup>3</sup> dargestellt. Hier lässt sich nicht wie im vorigen Fall eine Symmetrie zu einer Achse feststellen. Stattdessen ist diese Funktion <span style="color: blue">'''symmetrisch zum Ursprung'''</span>. Hierbei gilt der Zusammenhang <br /> | ||
| + | <span style="color: blue">'''f(x)=-f(-x)'''</span>. Das bedeutet, dass die Funktionswerte von f(x) und f(-x) vom Betrag her gleich sein müssen, aber unterschiedliche Vorzeichen haben. <br /> <br /> <br /> | ||
Dies lässt sich leicht durch ein Beispiel beweisen: <br /> | Dies lässt sich leicht durch ein Beispiel beweisen: <br /> | ||
| Zeile 57: | Zeile 46: | ||
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> Wie auch der Beweis der Achsensymmetrie wird dieser Beweis in der Regel allgemein geführt: <br /> | <div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> Wie auch der Beweis der Achsensymmetrie wird dieser Beweis in der Regel allgemein geführt: <br /> | ||
::f(x)=x<sup>3</sup> <br /> | ::f(x)=x<sup>3</sup> <br /> | ||
| − | ::<span style="color: blue">f(-x)</span>=(-x)<sup>3</sup> <br /> | + | ::<span style="color: blue">'''f(-x)'''</span>=(-x)<sup>3</sup> <br /> |
:: =-x<sup>3</sup> <br /> | :: =-x<sup>3</sup> <br /> | ||
| − | :: =<span style="color: blue">-f(x)</span> | + | :: =<span style="color: blue">'''-f(x)'''</span> |
| | | | ||
| valign="top" | | | valign="top" | | ||
| − | [[Bild:Graph Punktsymmetrie.png|410px|right]] | + | [[Bild:Graph Punktsymmetrie neu.png|410px|right]] |
|} | |} | ||
| Zeile 79: | Zeile 68: | ||
== <span style="color: blue">Ganzrationale Funktionen</span> == | == <span style="color: blue">Ganzrationale Funktionen</span> == | ||
| − | ''' <span style="color: blue">Aufgabe:</span>''' | + | ''' <span style="color: blue">Aufgabe:</span>''' <br /> |
| − | + | {| | |
| − | + | ! width="910" | | |
| − | + | |- | |
| − | + | | valign="top" | | |
| + | Unten siehst du 2 Applets mit Funktionsgraphen. Versuche, durch Verschieben der Regler Zusammenhänge zwischen der Veränderung der Exponenten und der Symmetrie der Graphen zu erkennen. Beachte dabei, wie die Regler eingestellt sind. <br /> | ||
| − | + | {| | |
| − | + | ! width="500" | | |
| − | + | ! width="20" | | |
| − | + | ! width="500" | | |
| − | + | |- | |
| − | + | | valign="top" | | |
| − | + | <ggb_applet width="825" height="503" version="3.2" ggbBase64="UEsDBBQACAAIAIqJNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVZLj9s2ED43v4LQKTmsTT0tA/YGaYoUAbbtwW0K9FCAksYyY4oUSGpX3l/fISnZjtP0hR5yIjUzHH4z38xQm9djJ8gjaMOV3EbxgkYEZK0aLtttNNj9XRm9vn+xaUG1UGlG9kp3zG6jdJFETj7w+xffbMxBPREmvMkHDk/byOoBImJ6DawxBwAbxHsmDMrZMHLBmT79VH2E2pqLIvh4L/vBzk7qrnngZv5c+vt6we13/JE3oIlQ9TYqckSOuw+gLa+Z2EYZDZIEw1rlnyhRlDrtQWn+rKR15hfne5QQYvgz4MnCyTZLH+cGhlrwhjPpgvE40IiQJ97YA0LIMnQJvD0g1pzGwVutlG52J2OhI+NvoBXenWD2kmS1ztOkyMpVGZHTpCmLRVzkCS1X6yQvcoRtEC8CybMF2tKUFsm6zLPURXSadXSRrYo4K7MizbJyXeThanjcgbXIpCFsBDPns9W8ud6/N98q0Zwp6BWX9i3r7aB9EaSTaGdP7jJMm3YhvpGtgEmWIEkHqI+VGnchbWlw/fOp90c8nKp9q4TSROMBF1k7rVVYvY3Debai3oZ6i8mHc3rWx+vEW/i1Cqu3ElwGaFPc6Rx0TOdruCFOgM5d7c7pEKwCrIWIDJLbh/kDa+Y4RRoH+x+HrsKeua6as8v4f3K5Wd6U2+YIWoIIRSWR10ENhjy64g3UeRwN1LzDz6CYEsIcWb8ggCBtoNUw4w4dF9LltfS6cG/Em+UMwmEwiLW2ODkwHuti+Z7JZ82cBAuTvBvk0e1Buo632G3b6B1yhxGRX7k4RqRhFk+5QQICOsC+s75i5NCB5vU5e13kECGMYQKTLSaUfvIoP0VuMn6hBtVfqCmcN/2B4W4xdatgJ5wo12nw3n5QzXTxZGeEHz0dx6F5V7ip2bERtYnbssooMVjY1Zhl+aBqn5EZ3jQtYkqdLR7K1iu3O2Ejl26z5yNc2vHPZ9Slwu0BS0mCMb4N7XXDMYmV4OnB6dOj3nk3PTjvftLP1qTHuH2znwsJqy8w8rfcyFtukq+Tm+I/UVNO1MQx/Tq5GfGJNe71nnO7xxd8RI/7l+MrsiXj7y+7V+TOrdKtdIEjd/kZq/tB+k6OLm6+GEt2E8u/5Xme/p8zTf8h0/QvMv0puutcLa9Hln/Vp7+a+z8AUEsHCAP636tpAwAABwkAAFBLAQIUABQACAAIAIqJNzwD+t+raQMAAAcJAAAMAAAAAAAAAAAAAAAAAAAAAABnZW9nZWJyYS54bWxQSwUGAAAAAAEAAQA6AAAAowMAAAAA" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | |
| + | |} | ||
| + | {| | ||
| + | ! width="500" | | ||
| + | ! width="20" | | ||
| + | ! width="500" | | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | <ggb_applet width="845" height="503" version="3.2" ggbBase64="UEsDBBQACAAIAMmJNzwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVZLb9swDD5vv0LQqR3QxM47QNxhD3Qo0G2H7AHsMEC2mUSLLBmS3Dr99aMeTrLsPezQkySSpj7yIykvnraVILegDVcyo2kvoQRkoUou1xlt7OpiRp9ePl6sQa0h14yslK6YzeiwN6BO3vDLx48WZqPuCBPe5AOHu4xa3QAlptbASrMBsEG8YsKgnDUtF5zp3dv8CxTWHBTBx7WsG9s5Karyhpvu2Pf31YLbl/yWl6CJUEVGJ2NEjrsPoC0vmMjoKAmSAYY1/VaJoqHTbpTm90paZ35wvkIJIYbfA345cbJF38e5gKYQvORMumA8DjQi5I6XdoMQJnN0CXy9QazjJA3eCqV0udwZCxVpP4FWeHc6cHnexdNs4k4GcbkLk6Q3Hk4nw9EomU2SQTpCw6gbIz3T6Wg+n0zQZDCdhRvgdgnWImGGsBZMl7a15uXx/to8V6LcZ7pWXNoXrLaN9lwPo2hpd+4uRKRdJM/kWkCUpcjFBoptrtplyM4wuH63q/0nHk6+fqGE0kRndDAeo0Fc87B6G4dzb5V4m8RbRB/O6V6fzgfewq95WL2V4DJAi3EPu6DTpLuGG+IELr9Yol06BMsBKaekkdzedAcsje0hUmf/pqlybI3j4ti7TP+Ty0X/pKoWW9ASRKgdibw2qjHk1tVooM7jKKHgFR6DIiaEObLeI4AgLWGtocMdGiuky2uT4/o8ES/6HQiHwSDWwuKAwHisi+UVk/eaOQnWJblq5NbtQbrGtthUGb1C7jAi8pGLLSUls/iVmxcgoAJsL+srRjYVaF7ss1dRhwhhNBHMsBdR+gGj/LA4yfiBGlT/pKZwrNQbhrtebErBdjg4jtPgvb1WZbw42hnhJ0zFcTZe+OFYsTajc7djuVGisbAsMMnyRhU+IR26OBNcO6MtfjOY+Z7HLnZBkRVv4dCMPx5Eh/q2GywkCcY4qmPyuhqXWAeeHBwxNer9MKnBefeIO2tSY9S+1fdlhLUX+PgtM/KUmfRhMjP9F2amkZkoenjUtPiMGvdCd6ld4SvdosfVWXtOMoKOyRPSfj6rzsmFW+U5Jf3vSF010rcxPbj5aSyjk1j+luZx6nl2Sxz8B6qTP6Q6+UWuv8V3nK3+8cTyb3f8d7n8ClBLBwgvokExUgMAAO0IAABQSwECFAAUAAgACADJiTc8L6JBMVIDAADtCAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAIwDAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | ||
| + | |} | ||
| + | {| | ||
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | Bei den Funktionen im oberen Applet handelt es sich um achsensymmetrische Funktionen, bei denen im unteren Applet um punktsymmetrische Funktionen. Betrachtet man die Exponenten der Funktionen, fällt auf, dass die <span style="color: blue">'''achsensymmetrischen Funktionen'''</span> nur <span style="color: blue">'''gerade Exponenten'''</span> enthalten. Deshalb werden sie gerade Funktionen genannt '''<span style="color: blue">(Zahlen ohne Variable x gelten als gerade)</span>'''. <br /> | ||
| + | Die <span style="color: blue">'''punktsymmetrischen Funktionen'''</span> enthalten nur <span style="color: blue">'''ungerade Exponenten'''</span> und heißen daher ungerade Funktionen. Wenn du dir also die Funktionen im oberen Applet anschaust, haben diese grundsätzlich gerade Exponenten, egal wie du die Regler verschiebst. | ||
| + | |} <br /> <br /> <br /> | ||
| + | {| | ||
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
<div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; ">''' <span style="color: red">Merke:</span>''' <br /> | <div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; ">''' <span style="color: red">Merke:</span>''' <br /> | ||
'''Eine gerade Funktion enthält nur geradzahlige Exponenten und ist achsensymmetrisch zur y-Achse.''' <br /> | '''Eine gerade Funktion enthält nur geradzahlige Exponenten und ist achsensymmetrisch zur y-Achse.''' <br /> | ||
| − | '''Eine ungerade Funktion enthält nur ungeradzahlige Exponenten und ist punktsymmetrisch zum Ursprung.''' </div> <br /> | + | '''Eine ungerade Funktion enthält nur ungeradzahlige Exponenten und ist punktsymmetrisch zum Ursprung.''' </div> |
| + | |} <br /> | ||
== <span style="color: blue">Beispielaufgaben</span> == | == <span style="color: blue">Beispielaufgaben</span> == | ||
| − | ''' <span style="color: blue">Aufgabe 1:</span>''' <br /> Untersuche folgende Funktionen rechnerisch auf Symmetrieeigenschaften. <br /> | + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 1:</span>''' <br /> Untersuche folgende Funktionen rechnerisch auf Symmetrieeigenschaften. <br /> |
| − | :a) f(x)= | + | :a) f(x)=3x<sup>5</sup> <br /> |
:b) f(x)=x<sup>4</sup>-2x<sup>2</sup>+3 <br /> | :b) f(x)=x<sup>4</sup>-2x<sup>2</sup>+3 <br /> | ||
:c) f(x)=x<sup>3</sup>-1 <br /> | :c) f(x)=x<sup>3</sup>-1 <br /> | ||
| Zeile 110: | Zeile 121: | ||
<popup name="Lösung"> | <popup name="Lösung"> | ||
a) <br /> | a) <br /> | ||
| − | :f(x)= | + | :f(x)=3x<sup>5</sup> <br /> |
| − | :f(-x)= | + | :f(-x)=3(-x)<sup>5</sup> <br /> |
| − | :f(-x)=- | + | :f(-x)=-3x<sup>5</sup> <br /> |
:<span style="color: red">f(-x)=-f(x)</span> oder <br /> | :<span style="color: red">f(-x)=-f(x)</span> oder <br /> | ||
:<span style="color: red">f(x)=-f(-x)</span> <br /> | :<span style="color: red">f(x)=-f(-x)</span> <br /> | ||
| Zeile 129: | Zeile 140: | ||
| − | </popup> <br /> <br /> | + | </popup> </div> <br /> <br /> |
| − | ''' <span style="color: blue">Aufgabe 2:</span>''' <br /> Überprüfe, ob die Funktionen gerade oder ungerade sind. | + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 2:</span>''' <br /> Überprüfe, ob die Funktionen gerade oder ungerade sind. |
:a) f(x)=11x<sup>8</sup>-6x<sup>6</sup>+5x<sup>2</sup>-3 <br /> | :a) f(x)=11x<sup>8</sup>-6x<sup>6</sup>+5x<sup>2</sup>-3 <br /> | ||
| Zeile 150: | Zeile 161: | ||
:2 : gerade <br /> | :2 : gerade <br /> | ||
:→ Weder gerade noch ungerade | :→ Weder gerade noch ungerade | ||
| − | </popup> <br /> <br /> | + | </popup> </div> <br /> <br /> |
| − | ''' <span style="color: blue">Aufgabe 3:</span>''' <br /> | + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 3:</span>''' <br /> |
Richtig oder falsch? <br /> <br /> | Richtig oder falsch? <br /> <br /> | ||
<quiz display="simple"> | <quiz display="simple"> | ||
| Zeile 168: | Zeile 179: | ||
{Die Funktion f(x)=x<sup>3</sup>-1 ist ungerade.} | {Die Funktion f(x)=x<sup>3</sup>-1 ist ungerade.} | ||
| − | - | + | - Richtig |
+ Falsch | + Falsch | ||
| Zeile 174: | Zeile 185: | ||
+ Richtig | + Richtig | ||
- Falsch | - Falsch | ||
| − | </quiz> | + | </quiz> </div> |
<br> | <br> | ||
| − | + | |} | |
[[Facharbeit Florian Wilk/Grenzwerte im Unendlichen|Weiter zum Kapitel Grenzwerte im Unendlichen]] | [[Facharbeit Florian Wilk/Grenzwerte im Unendlichen|Weiter zum Kapitel Grenzwerte im Unendlichen]] | ||
Aktuelle Version vom 27. Januar 2010, 16:13 Uhr
Symmetrie von FunktionsgraphenAchsensymmetrie
Punktsymmetrie zum Ursprung
Ganzrationale Funktionen Aufgabe:
Weiter zum Kapitel Grenzwerte im Unendlichen
|