Integralberechnung: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Quelle auf Integralseite eingefügt) |
("Mal" Zeichen verändert) |
||
| Zeile 30: | Zeile 30: | ||
::{{Lösung versteckt|1= | ::{{Lösung versteckt|1= | ||
| − | ::<math>\int f (t)\,dt = \frac{1}{16}t^4 - \frac{a | + | ::<math>\int f (t)\,dt = \frac{1}{16}t^4 - \frac{a \cdot t^3}{3} + \frac{a^2 \cdot t^2}{2} + c = F (t)</math> |
::Die obere Grenze ist: 6 <small> ''Nach den ersten sechs Monaten''</smalL> | ::Die obere Grenze ist: 6 <small> ''Nach den ersten sechs Monaten''</smalL> | ||
| Zeile 36: | Zeile 36: | ||
::Die untere Grenze ist: 0 | ::Die untere Grenze ist: 0 | ||
| − | ::<math>\int_{0}^{6} f (t)\,dt = </math> <math>\left[ \frac{1}{16}t^4 - \frac{3 | + | ::<math>\int_{0}^{6} f (t)\,dt = </math> <math>\left[ \frac{1}{16}t^4 - \frac{3 \cdot t^3}{3} + \frac{3^2 \cdot t^2}{2}\right ]_{0}^{6} = 27 - 0 = 27</math> |
| − | ::<u>Für a = 3 fließen in den ersten sechs Monaten 27 | + | ::<u>Für a = 3 fließen in den ersten sechs Monaten 27 \cdot 10<sup>9</sup> Liter Wasser durch den Fluss.</u> (<small> 27 \cdot 10<sup>6</sup> m<sup>3</sup> = 27 \cdot 10<sup>9</sup> Liter</small>) |
}} | }} | ||
Version vom 27. Januar 2010, 14:43 Uhr
Berechnung des Wasservolumens in den ersten sechs Monaten
Ermittle für a = 3 wie viel Liter Wasser in den ersten sechs Monaten durch den Fluss fließen.
|
|
- Gebe die Funktion F (t) an und errechne mit ihr für a = 3, wieviel Liter in den ersten sechs Monaten durch den Fluss geflossen sind.
- Die obere Grenze ist: 6 Nach den ersten sechs Monaten
- Die untere Grenze ist: 0
- Für a = 3 fließen in den ersten sechs Monaten 27 \cdot 109 Liter Wasser durch den Fluss. ( 27 \cdot 106 m3 = 27 \cdot 109 Liter)
- Falls du mit der Integration noch Schwierigkeiten haben solltest, gibt es hier einen nützlichen Link.
Hier geht's zur Aufgabe: Volumengleicheit zweier verschiedener Funktionen bis zum Zeitpunkt t0,
Hier geht's zurück zur Übersicht
Quellen
- ↑ Barth, Friedrich / Mühlbauer, Paul / Nikol, Friedrich / Wörle Karl, Mathematische Formeln und Definitionen, München
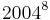 , S.66
, S.66
- ↑ Integrierbarkeit einer Funktion
![\int_{a}^{b} x^n \,dx = \left[ \frac{x^{n+1}}{n+1} \right]_{a}^{b}](/images/math/c/4/e/c4e09d0a32630fc2d68d22072dd7ccd8.png)
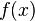 im Intervall[]
im Intervall[] ![\left [ a , b \right ]](/images/math/f/9/4/f944498af9d6490b5599ba93146f9db8.png) ist aber nicht immer definiert, sondern nur dann, wenn die Funktion im Intervall
ist aber nicht immer definiert, sondern nur dann, wenn die Funktion im Intervall 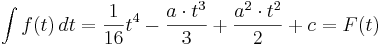
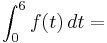
![\left[ \frac{1}{16}t^4 - \frac{3 \cdot t^3}{3} + \frac{3^2 \cdot t^2}{2}\right ]_{0}^{6} = 27 - 0 = 27](/images/math/f/7/1/f71e9edb8b764bb660fd0ac14ab9482b.png)

