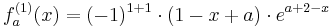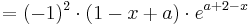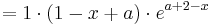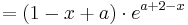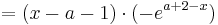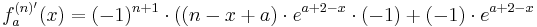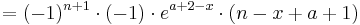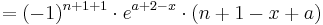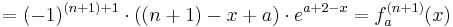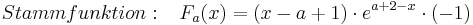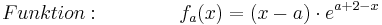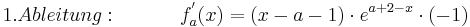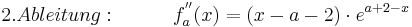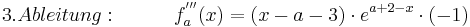Lösung von Teilaufgabe e: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: == Beweisführung zur n-ten Ableitung der Funktion <math> f_a</math> durch vollständige Induktion== [http://de.wikibooks.org/wiki/Mathe_f%C3%BCr_Nicht-Freaks:_Vollst%...) |
(→Beweisführung durch Betrachtung der Ableitungen von f_a) |
||
| (9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
| − | == Beweisführung zur n-ten Ableitung der Funktion < | + | == Beweisführung zur n-ten Ableitung der Funktion f<sub>a</sub> durch vollständige Induktion== |
| − | + | ||
| − | + | ||
Beweise, dass<br /> | Beweise, dass<br /> | ||
| Zeile 7: | Zeile 5: | ||
die n-te Ableitung von <math>f_a (x) = ( x - a )\cdot e^{a+2-x}</math>ist. (Behauptung) | die n-te Ableitung von <math>f_a (x) = ( x - a )\cdot e^{a+2-x}</math>ist. (Behauptung) | ||
| − | + | [http://de.wikibooks.org/wiki/Mathe_f%C3%BCr_Nicht-Freaks:_Vollst%C3%A4ndige_Induktion Hilfe zur vollständigen Induktion] | |
| + | |||
| − | 1. Induktionsanfang: | + | === 1. Induktionsanfang: === |
Die erste Ableitung ist: <math> f^{'}_a (x) = ( x - a - 1 )\cdot (-e^{a + 2 - x}) </math> (siehe Teilaufgabe a / Extrempunkte)<br /> | Die erste Ableitung ist: <math> f^{'}_a (x) = ( x - a - 1 )\cdot (-e^{a + 2 - x}) </math> (siehe Teilaufgabe a / Extrempunkte)<br /> | ||
| − | Die Behauptung stimmt | + | |
| + | Die Behauptung stimmt damit überein: | ||
::<math>f_a^{(1)}(x)=(-1)^{1+1}\cdot(1-x+a)\cdot e^{a+2-x}</math><br /> | ::<math>f_a^{(1)}(x)=(-1)^{1+1}\cdot(1-x+a)\cdot e^{a+2-x}</math><br /> | ||
| + | |||
::::<math>=(-1)^{2}\cdot(1-x+a)\cdot e^{a+2-x}</math><br /> | ::::<math>=(-1)^{2}\cdot(1-x+a)\cdot e^{a+2-x}</math><br /> | ||
| + | |||
::::<math>=1\cdot(1-x+a)\cdot e^{a+2-x}</math><br /> | ::::<math>=1\cdot(1-x+a)\cdot e^{a+2-x}</math><br /> | ||
| + | |||
::::<math>=(1-x+a)\cdot e^{a+2-x}</math><br /> | ::::<math>=(1-x+a)\cdot e^{a+2-x}</math><br /> | ||
| + | |||
::::<math>=(x-a-1)\cdot (-e^{a+2-x})</math><br /> | ::::<math>=(x-a-1)\cdot (-e^{a+2-x})</math><br /> | ||
| − | 2. Induktionsschritt: | + | |
| + | === 2. Induktionsschritt: === | ||
Anfangsgleichung: <math>f_a^{(n)}(x)=(-1)^{n+1}\cdot(n-x+a)\cdot e^{a+2-x}</math> | Anfangsgleichung: <math>f_a^{(n)}(x)=(-1)^{n+1}\cdot(n-x+a)\cdot e^{a+2-x}</math> | ||
| − | Zielgleichung: <math>f_a^{(n+1)}(x)=(-1)^{(n+1)+1}\cdot((n+1)-x+a)\cdot e^{a+2-x}</math> | + | Zielgleichung: <math>f_a^{(n+1)}(x)=(-1)^{(n+1)+1}\cdot((n+1)-x+a)\cdot e^{a+2-x}</math> |
Wenn die n-te Ableitung von f<sub>a</sub> für n stimmt, muss sie auch für n+1 stimmen.<br /> | Wenn die n-te Ableitung von f<sub>a</sub> für n stimmt, muss sie auch für n+1 stimmen.<br /> | ||
| + | |||
Dies soll nun bewiesen werden.<br /> | Dies soll nun bewiesen werden.<br /> | ||
| − | |||
| + | Der Beweis stimmt, wenn <math>f_a^{(n)'}(x)= f_a^{(n+1)}(x)</math><br /> | ||
| + | Um die erste Ableitung zu bekommen, muss man hier die Produktregel verwenden | ||
| + | [[http://de.wikipedia.org/wiki/Produktregel Hilfe zur Produktregel]]<br /> | ||
| + | :<math>f_a^{(n)'}(x)= (-1)^{n+1}\cdot((n-x+a)\cdot e^{a+2-x}\cdot (-1) + (-1)\cdot e^{a+2-x}</math><br /> | ||
| + | :::<math>=(-1)^{n+1}\cdot (-1)\cdot e^{a+2-x}\cdot (n-x+a+1)</math><br /> | ||
| + | :::<math>=(-1)^{n+1+1}\cdot e^{a+2-x}\cdot (n+1-x+a)</math><br /> | ||
| + | :::<math>=(-1)^{(n+1)+1}\cdot ((n+1)-x+a)\cdot e^{a+2-x} = f_a^{(n+1)}(x)</math><br /> | ||
| − | + | == Beweisführung durch Betrachtung der Ableitungen von <math>f_a</math> == | |
| + | |||
| + | Durch Betrachtung der Ableitungen und Integrale von <math>f_a (x)\,</math> lässt sich eine gewisse Regel erkennen.<br /> | ||
| + | |||
| + | :<math>Stammfunktion: \;\;\; F_a (x) = ( x - a + 1 )\cdot e^{a + 2 - x}\cdot (-1) </math> <br /> | ||
| + | :<math>Funktion: \;\;\;\;\;\;\;\;\;\;\;\;\;\; f_a (x) = ( x - a )\cdot e^{a + 2 - x} </math> <br /> | ||
| + | :<math>1. Ableitung: \;\;\;\;\;\;\;\; \;\;\; f^{'}_a (x) = ( x - a - 1 )\cdot e^{a + 2 - x}\cdot (-1) </math> <br /> | ||
| + | :<math>2. Ableitung: \;\;\;\; \;\;\;\;\;\;f^{''}_a (x) = ( x - a - 2 )\cdot e^{a + 2 - x} </math> <br /> | ||
| + | :<math>3. Ableitung: \;\;\;\;\;\;\;\;\;\; f^{'''}_a (x) = ( x - a - 3 )\cdot e^{a + 2 - x}\cdot (-1) </math> <br /> | ||
| + | |||
| + | Aus den gezeigten Ableitungen lässt sich erkennen, ausgehend von der Stammfunktion, dass für jede Ableitung der erste Faktor dieses Produkts (die Variablen in der Klammer) um eins abnimmt.<br /> Außerdem wird bei jeder zweiten Ableitung eine Änderung des Vorzeichens verzeichnet. Das heißt, jede zweite Ableitung wird mit (-1) multipliziert. | ||
| + | |||
| + | :<math>\sum_{1}^\infty (-1)^{n}\cdot(x-a-n)\cdot e^{a+2-x}=</math><br /> | ||
| + | :=<math>\sum_{1}^\infty (-1)^{n}\cdot(-1)\cdot(n-x+a)\cdot e^{a+2-x}</math><br /> | ||
| + | :=<math>\sum_{1}^\infty (-1)^{n+1}\cdot(n-x+a)\cdot e^{a+2-x} = f_a^{(n)}(x)</math><br /> | ||
| + | |||
| + | Die durch die Überlegung entwickelte Formel für die n-te Ableitung von <math>f_a(x)\,</math> stimmt mit derjenigen, welche bewiesen werde sollte überein.<br /> | ||
| + | <math>y=f_a^{(n)}(x)=(-1)^{n+1}\cdot(n-x+a)\cdot e^{a+2-x}</math> | ||
| + | |||
| + | Diese Methode der Beweisführung ist kein echter Beweis, da nie alle Ableitungen in Betracht gezogen werden können, sondern nur ein kleiner Teil. | ||
| + | Sie ist eher zum besseren Verstehen und Vorstellen vorhanden. | ||
Aktuelle Version vom 26. Januar 2010, 21:36 Uhr
Inhaltsverzeichnis |
Beweisführung zur n-ten Ableitung der Funktion fa durch vollständige Induktion
Beweise, dass
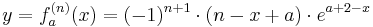 die n-te Ableitung von
die n-te Ableitung von 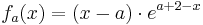 ist. (Behauptung)
ist. (Behauptung)
Hilfe zur vollständigen Induktion
1. Induktionsanfang:
Die erste Ableitung ist: 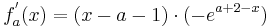 (siehe Teilaufgabe a / Extrempunkte)
(siehe Teilaufgabe a / Extrempunkte)
Die Behauptung stimmt damit überein:
2. Induktionsschritt:
Anfangsgleichung: 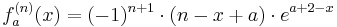
Zielgleichung: 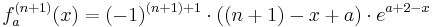
Wenn die n-te Ableitung von fa für n stimmt, muss sie auch für n+1 stimmen.
Dies soll nun bewiesen werden.
Der Beweis stimmt, wenn 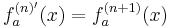
Um die erste Ableitung zu bekommen, muss man hier die Produktregel verwenden
[Hilfe zur Produktregel]
Beweisführung durch Betrachtung der Ableitungen von 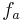
Durch Betrachtung der Ableitungen und Integrale von 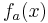 lässt sich eine gewisse Regel erkennen.
lässt sich eine gewisse Regel erkennen.
Aus den gezeigten Ableitungen lässt sich erkennen, ausgehend von der Stammfunktion, dass für jede Ableitung der erste Faktor dieses Produkts (die Variablen in der Klammer) um eins abnimmt.
Außerdem wird bei jeder zweiten Ableitung eine Änderung des Vorzeichens verzeichnet. Das heißt, jede zweite Ableitung wird mit (-1) multipliziert.
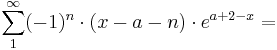
- =
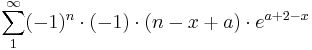
- =
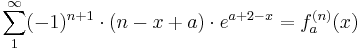
Die durch die Überlegung entwickelte Formel für die n-te Ableitung von 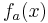 stimmt mit derjenigen, welche bewiesen werde sollte überein.
stimmt mit derjenigen, welche bewiesen werde sollte überein.
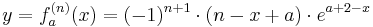
Diese Methode der Beweisführung ist kein echter Beweis, da nie alle Ableitungen in Betracht gezogen werden können, sondern nur ein kleiner Teil. Sie ist eher zum besseren Verstehen und Vorstellen vorhanden.