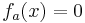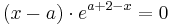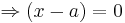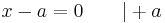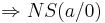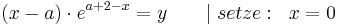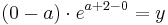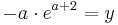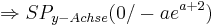Lösung: Schnittpunkte mit den Koordinatenachsen: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Schnittpunkte mit den Koordinatenachsen) |
(→2. Schnittpunkt mit der y-Achse) |
||
| (12 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 3: | Zeile 3: | ||
=== Schnittpunkte mit den Koordinatenachsen === | === Schnittpunkte mit den Koordinatenachsen === | ||
| + | |||
| Zeile 8: | Zeile 9: | ||
====1. Nullstellen ==== | ====1. Nullstellen ==== | ||
| − | + | Nullstellen (Schnittpunkte mit der x-Achse) erhält man, indem man die Funktion gleich Null setzt. | |
| − | + | ||
| − | + | :<math>f_a (x) = 0\;</math><br /> | |
| + | |||
| + | :<math>( x - a )\cdot e^{a+2-x} = 0</math><br /> | ||
| + | |||
| + | Da die e-Funktion ( in diesem Fall e<sup>a + 2 - x</sup>) immer streng monoton steigend und<br /> immer positiv ist, kann hier nur der Faktor ( x - a ) den Wert Null annehmen. | ||
| − | + | :<math>\Rightarrow ( x - a ) = 0</math><br /> | |
| − | + | ||
| − | + | ::<math>x - a = 0 \;\;\;\;\;\;\; | +a</math><br /> | |
| + | |||
| + | :::<math> x = a\;</math><br /> | ||
| − | + | ||
| + | :<math>\Rightarrow NS ( a / 0 )</math><br /> | ||
| + | |||
Für <math>a < 0\;</math> folgt: <math>\;\;\;\; NS ( <0 / 0 )\;</math><br /> | Für <math>a < 0\;</math> folgt: <math>\;\;\;\; NS ( <0 / 0 )\;</math><br /> | ||
| Zeile 22: | Zeile 31: | ||
Für <math>a = 0\;</math> folgt: <math>\;\;\;\; NS ( 0 / 0 )\;</math><br /> | Für <math>a = 0\;</math> folgt: <math>\;\;\;\; NS ( 0 / 0 )\;</math><br /> | ||
| + | ====2. Schnittpunkt mit der y-Achse ==== | ||
| + | Schnittpunkte mit der y-Achse erhält man, indem man für x = 0 setzt. | ||
| − | == | + | :<math>( x - a )\cdot e^{a+2-x} = y \;\;\;\;\;\;\; |\; setze:\;\; x = 0</math> <br /> |
| + | |||
| + | :<math>( 0 - a )\cdot e^{a+2-0} = y</math><br /> | ||
| + | |||
| + | ::: <math>-a\cdot e^{a+2} = y</math><br /> | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | :<math>\Rightarrow SP_{y-Achse} (0 / -a e^{a+2} )</math> | |
| Zeile 37: | Zeile 48: | ||
Für <math>a > 0\;</math> folgt: <math> \;\;\;\;SP_{y-Achse}( 0 / <0 )\;</math><br /> | Für <math>a > 0\;</math> folgt: <math> \;\;\;\;SP_{y-Achse}( 0 / <0 )\;</math><br /> | ||
Für <math>a = 0\;</math> folgt: <math> \;\;\;\;SP_{y-Achse}( 0 / 0 )\;</math><br /> | Für <math>a = 0\;</math> folgt: <math> \;\;\;\;SP_{y-Achse}( 0 / 0 )\;</math><br /> | ||
| + | |||
| + | ==== Grafik zu den Schnittpunkten mit den Koordinatenachsen ==== | ||
| + | |||
| + | |||
| + | <ggb_applet width="583" height="377" version="3.2" ggbBase64="UEsDBBQACAAIAC2GOjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1szVZRj9s2DH5ef4Xgp2RrHNuJEweIr+i6lwLXdkC2PuxhhWwziXq2ZUjynXO/vhRlJ7n0ut5twzD4wTJJUeRH8pPXr7qqZLegtJB16oV+4DGoc1mIepd6rdlOEu/V1Yv1DuQOMsXZVqqKm9Sb+ZFn5a24evHDWu/lHeMlmXwUcJd6W15q8JhuFPBC7wHMAzlvO1EKrg4fss+QG31SOCdv66bFU4xqUZZXxbXQw+eUDmxKYX4Rt6IAxUqZp94ixtBx9RGUETkvU28eOEmUetGFEkUzq91LJe5lbaz5yfkWJYxpcQ+ISGRl6ykluoY2L0UheG2ToTjQiLE7UZh96sXJDF2C2O0tQMvYeculVMXmoA1UrPsDlMRwwsRfxOE8mK/iZLFcLj12cJpwMfMXqzAZngg9agwYI5nH/jw+exa46ZsqOhluN2AMVlIz3oEe4NwpURzxth9v9c+yPIkaKWrzhjemVdQFs160MQd7GMKmbIqv610JvSzCIu0hv8lkt3GwzZzr3w4NbaF4st0bWUrFlC1IjAb9O3NvsrGBHq0CsgnIovdhnR714SoiC3pn7k1WpahdaH3i4ZB1GAzHCM2sAJ3b5h2wKXkG2Asea2throcP7JmbPtPQ2b9vqwyH5rxrji7Df8nlenrRbusbUDWUrqlqLGwrW81ubfO60lEcBeSiwk+n6AHhtli/YwBOWsBOwRC3mzgHF2mD88a9EK+nQxA2Bo2x5gapA/MxNhc72Qanyq4KbqzEjk0JFeBMGeqGuq1AifyIDPfsaXhEOxzk91ETrUhiiAs0T7Cj+hv9glzS7Ll1F/ZdwQ/IFucpkrd3sugP7u10SbRSCWTESWwpseIdjrdd8UzLsjWwyRHA+lrm3BBzuuh6IgiDwNp2lmXs4oCbabEVHZwG7XH2OfWu2WOT1KA1DZg5HyVeY40JeOSVxuWIZAvg+m+wZQ3mTEN8bBDsKleN79YFLusS+UtkJMtKyTxeBfP4kSr1qf0XZSIwneRsCoeL5aHiQdYdXkraXnhDmNtPHK+9rqHVqBuzlI06NmF8zH5k8OeIs59Y5Aco6cYem36F3LataQq8c4dPruVzu3zgzq8BDJ4IYPDkTvtr3N5vethG/CXD48fDXrovHkOqV5z2/9MxJzD+LgDEcNrOqaUcO6Y0pffuR4hM3M1nb3naOPs+KJtfPx0GWNDdSzYZXfTR+Lk4kcv/DVKO0CahnwRxEESL1SpJFkmEdPAs5Kbn9wf9YvX/mFdfAFBLBwhTLYKwrwMAAJUKAABQSwECFAAUAAgACAAthjo8Uy2CsK8DAACVCgAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAOkDAAAAAA==" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> | ||
Aktuelle Version vom 26. Januar 2010, 19:33 Uhr
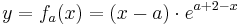 mit
mit  ;
; 
Inhaltsverzeichnis |
Schnittpunkte mit den Koordinatenachsen
1. Nullstellen
Nullstellen (Schnittpunkte mit der x-Achse) erhält man, indem man die Funktion gleich Null setzt.
Da die e-Funktion ( in diesem Fall ea + 2 - x) immer streng monoton steigend und
immer positiv ist, kann hier nur der Faktor ( x - a ) den Wert Null annehmen.
Für 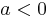 folgt:
folgt: 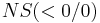
Für 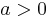 folgt:
folgt: 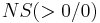
Für 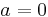 folgt:
folgt: 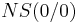
2. Schnittpunkt mit der y-Achse
Schnittpunkte mit der y-Achse erhält man, indem man für x = 0 setzt.
Für 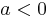 folgt:
folgt: 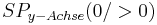
Für 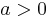 folgt:
folgt: 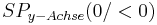
Für 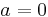 folgt:
folgt: 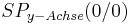
Grafik zu den Schnittpunkten mit den Koordinatenachsen