Integralberechnung: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 1: | Zeile 1: | ||
===Berechnung des Wasservolumens in den ersten sechs Monaten=== | ===Berechnung des Wasservolumens in den ersten sechs Monaten=== | ||
| − | '''''<span style="color: darkorange">Ermittle für a = 3 | + | '''''<span style="color: darkorange">Ermittle für a = 3 wie viel Liter Wasser in den ersten sechs Monaten durch den Fluss fließen.</span> |
{| | {| | ||
| Zeile 23: | Zeile 23: | ||
|width=5px| | |width=5px| | ||
|valign="top" | | |valign="top" | | ||
| − | <ggb_applet width="369" height="458" version="3.2" ggbBase64=" | + | <ggb_applet width="369" height="458" version="3.2" ggbBase64="UEsDBBQACAAIAES6OTwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1stVZLj9MwED6zv8LKaQFtm0efUruIx2WlhT0UOHBAcpJJY9axI9vZTffXM36k7RYBiwD1YHs8nsc330y6etU3nNyB0kyKdZSM4oiAKGTJxHYddaa6WESvLs9WW5BbyBUllVQNNesoG6WRlXfs8uzZStfynlDuVD4zuF9HFeUaIqJbBbTUNYB5JKddzzijaneTf4PC6MOFN3Il2g69GNWhrGjKa6aH49g6rKQwhGj2ABh0amWrsYtlBV3BWcmosP5cbKhEyD0rTY1hz5YRqYFtazQ3mc68tUJKVW522kBD+i+gJN4tR4vk+BeRXbiJJ6PFYpZN5tkyXi6zGWZZUI6BpIsRSg6/ZI6Pwl2yGGXzOJ1NJvPJLMW3mXcNdxswBtHWhPagh5S3ipXH+yv9RvJyj1IrmTBvaWs65QqVBdHG7KwzLKKyKb4WWw5BliKONRS3uew3HrbMm/64a90TF06+fSu5VEThg+kUFcKa+9Xp2Dj3WrHTiZ1GsGGN7u+TZeo03Jr71WlxJnxoIe9kSDqJBzdMEytA45ZfAxyc5sDXUUQ6wcz1cDCsuA2ZJl7/Q9fkyOvhmVV4hyyiogBP9Mdekv/nZTU+IeXqFpQA7qknsPqd7DS5o3wosAuthII1ePQXATZqS/oJY/LSErYKgn5oHQ+qu42P6X0iXo2HIGwMGsMvDM4AzMDY9GyLmloquyupsRLbXBwawM4zjjOia0CxYg8Wjaw3dNEFR9mAspsP0rX6CcCHlsbrn7AKh0JbU9yNksAdugP1KEVn7b0sg+OgpxF0VGzYMNoa2mMD2x3NteSdgU2B+IlrWVDjJqAPLkyLJI6tLr6Zu80OU5raTcV6OHQjwsQesI70UT4HgpsaWSFAa9eF5rjfqMASO9xx+LQhSt2Cte72gzZpMWnX63uGIK18OWxhehy02g7xAdgKB3mPFqvz/jlZEzRGxgRTJy9I//UcK/OcXBDqT6k9vSQ07FAWkfEP5a464SgSHVw8Oc9/RYD4iQSIn1yDYxQL2TRUlETQBq+vhMHuotxlyewHidDYA4oRJT4cQlO06GClIY3ODKq5dxDM/rZ/8tP+Sed/10BJnP6A4PSXCN5UlQZjGX+RJo7wk/mvOuwPAR4fjxr3zQ7/Ky6/A1BLBwhdA5TzWAMAAIkIAABQSwECFAAUAAgACABEujk8XQOU81gDAACJCAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAJIDAAAAAA==" framePossible = "true" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> |
|} | |} | ||
| Zeile 29: | Zeile 29: | ||
::{{Lösung versteckt|1= | ::{{Lösung versteckt|1= | ||
| − | ::<math>\ | + | ::<math>\int f (t)\,dt = \frac{1}{16}t^4 - \frac{a*t^3}{3} + \frac{a^2*t^2}{2} + c = F (t)</math> |
::Die obere Grenze ist: 6 <small> ''Nach den ersten sechs Monaten''</smalL> | ::Die obere Grenze ist: 6 <small> ''Nach den ersten sechs Monaten''</smalL> | ||
| Zeile 41: | Zeile 41: | ||
| − | ::Falls du mit der Integration noch Schwierigkeiten haben solltest, [http://de.sevenload.com/sendungen/Nachhilfe-2-0/folgen/s8j162f-Flaeche-berechnen-Grenzen-gegeben-Integralrechnung hier] | + | ::Falls du mit der Integration noch Schwierigkeiten haben solltest, gibt es [http://de.sevenload.com/sendungen/Nachhilfe-2-0/folgen/s8j162f-Flaeche-berechnen-Grenzen-gegeben-Integralrechnung hier] einen nützlichen Link. |
Version vom 25. Januar 2010, 23:19 Uhr
Berechnung des Wasservolumens in den ersten sechs Monaten
Ermittle für a = 3 wie viel Liter Wasser in den ersten sechs Monaten durch den Fluss fließen.
|
|
- Gebe die Funktion F (t) an und errechne mit ihr für a = 3, wieviel Liter in den ersten sechs Monaten durch den Fluss geflossen sind.
- Die obere Grenze ist: 6 Nach den ersten sechs Monaten
- Die untere Grenze ist: 0
- Für a = 3 fließen in den ersten sechs Monaten 27*109 Liter Wasser durch den Fluss. ( 27*106 m3 = 27*109 Liter)
- Falls du mit der Integration noch Schwierigkeiten haben solltest, gibt es hier einen nützlichen Link.
Hier geht's zur Aufgabe: Volumengleicheit zweier verschiedener Funktionen bis zum Zeitpunkt t0,
![\int_{a}^{b} x^n \,dx = \left[ \frac{x^{n+1}}{n+1} \right]_{a}^{b}](/images/math/c/4/e/c4e09d0a32630fc2d68d22072dd7ccd8.png)
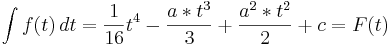
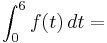
![\left[ \frac{1}{16}t^4 - \frac{3*t^3}{3} + \frac{3^2*t^2}{2}\right ]_{0}^{6} = 27 - 0 = 27](/images/math/4/9/a/49a1f445fbc0fa11cad513f8131a8bd7.png)

