Symmetrie von Funktionsgraphen: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(→‎Beispielaufgaben)
(→‎Punktsymmetrie zum Ursprung)
Zeile 37: Zeile 37:
 
| valign="top" |
 
| valign="top" |
 
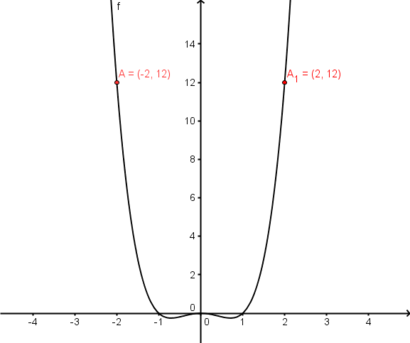
Im nebenstehenden Koordinatensystem ist der Graph der Funktion <br />
 
Im nebenstehenden Koordinatensystem ist der Graph der Funktion <br />
−
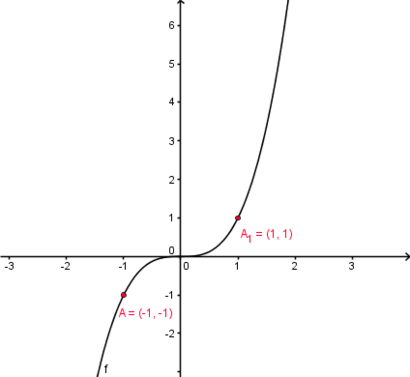
f(x)=x<sup>3</sup> dargestellt. Hier lässt sich nicht wie im vorigen Fall eine Symmetrie zu einer Achse feststellen. Stattdessen ist diese Funktion <span style="color: blue">'''symmetrisch zum Ursprung'''</span>. Hierbei gilt der Zusammenhang <span style="color: blue">'''f(x)=-f(-x)'''</span>. Das bedeutet, dass die Funktionswerte von f(x) und f(-x) vom Betrag her gleich sein müssen, aber unterschiedliche Vorzeichen haben. <br /> <br /> <br />
+
f(x)=x<sup>3</sup> dargestellt. Hier lässt sich nicht wie im vorigen Fall eine Symmetrie zu einer Achse feststellen. Stattdessen ist diese Funktion <span style="color: blue">'''symmetrisch zum Ursprung'''</span>. Hierbei gilt der Zusammenhang <br />
 +
<span style="color: blue">'''f(x)=-f(-x)'''</span>. Das bedeutet, dass die Funktionswerte von f(x) und f(-x) vom Betrag her gleich sein müssen, aber unterschiedliche Vorzeichen haben. <br /> <br /> <br />
  
 
Dies lässt sich leicht durch ein Beispiel beweisen: <br />  
 
Dies lässt sich leicht durch ein Beispiel beweisen: <br />  

Version vom 24. Januar 2010, 12:37 Uhr

Inhaltsverzeichnis

Symmetrie von Funktionsgraphen

Achsensymmetrie

Im nebenstehenden Koordinatensystem ist der Graph der Funktion
f(x)=x4-x2 abgebildet. Bei der Betrachtung des Graphen fällt auf, dass er auf beiden Seiten der y-Achse den gleichen Verlauf nimmt. Wenn man also einen Punkt des Graphen an der y-Achse spiegelt, liegt der Spiegelpunkt ebenfalls auf dem Graphen. Dies wird als Achsensymmetrie zur y-Achse bezeichnet. Zum Beweis dieser Symmetrie nutzt man den Zusammenhang f(x)=f(-x). Wenn also das Einsetzen von f(x) und f(-x) den gleichen Funktionswert ergibt, handelt es sich um einen achsensymmetrischen Graphen.

Setzt man beispielsweise in diesem Fall 2 und -2 in den Funktionsterm ein, so kommt beide Male das gleiche Ergebnis dabei heraus:

f(2)=24-22=12
f(-2)=(-2)4-(-2)2=12

In der Regel wird dieser Beweis allerdings allgemein durchgeführt, indem man –x in den Funktionsterm einsetzt:

f(x)=x4-x2
f(-x)=(-x)4-(-x)2
    =x4-x2
    =f(x)




Graph Achsensymmetrie neu.png

Punktsymmetrie zum Ursprung

Im nebenstehenden Koordinatensystem ist der Graph der Funktion
f(x)=x3 dargestellt. Hier lässt sich nicht wie im vorigen Fall eine Symmetrie zu einer Achse feststellen. Stattdessen ist diese Funktion symmetrisch zum Ursprung. Hierbei gilt der Zusammenhang
f(x)=-f(-x). Das bedeutet, dass die Funktionswerte von f(x) und f(-x) vom Betrag her gleich sein müssen, aber unterschiedliche Vorzeichen haben.


Dies lässt sich leicht durch ein Beispiel beweisen:

f(1)=13=1
f(-1)=(-1)3=-1

Wie auch der Beweis der Achsensymmetrie wird dieser Beweis in der Regel allgemein geführt:
f(x)=x3
f(-x)=(-x)3
    =-x3
    =-f(x)
Graph Punktsymmetrie neu.png



Merke:

Achsensymmetrie zur y-Achse:       f(x)=-f(x)

Punktsymmetrie zum Ursprung:     f(-x)=-f(x)

Ganzrationale Funktionen

Aufgabe:

Unten siehst du 2 Applets mit Funktionsgraphen. Versuche, durch Verschieben der Regler Zusammenhänge zwischen der Veränderung der Exponenten und der Symmetrie der Graphen zu erkennen. Beachte dabei, wie die Regler eingestellt sind.


Bei den Funktionen im oberen Applet handelt es sich um achsensymmetrische Funktionen, bei denen im unteren Applet um punktsymmetrische Funktionen. Betrachtet man die Exponenten der Funktionen, fällt auf, dass die achsensymmetrischen Funktionen nur gerade Exponenten enthalten. Deshalb werden sie gerade Funktionen genannt (Zahlen ohne Variable x gelten als gerade).
Die punktsymmetrischen Funktionen enthalten nur ungerade Exponenten und heißen daher ungerade Funktionen. Wenn du dir also die Funktionen im oberen Applet anschaust, haben diese grundsätzlich gerade Exponenten, egal wie du die Regler verschiebst.




Merke:

Eine gerade Funktion enthält nur geradzahlige Exponenten und ist achsensymmetrisch zur y-Achse.

Eine ungerade Funktion enthält nur ungeradzahlige Exponenten und ist punktsymmetrisch zum Ursprung.

Beispielaufgaben

Aufgabe 1:
Untersuche folgende Funktionen rechnerisch auf Symmetrieeigenschaften.
a) f(x)=cosx
b) f(x)=x4-2x2+3
c) f(x)=x3-1




Aufgabe 2:
Überprüfe, ob die Funktionen gerade oder ungerade sind.
a) f(x)=11x8-6x6+5x2-3
b) f(x)=4x7+x5-3x3
c) f(x)=5x3-2




Aufgabe 3:

Richtig oder falsch?

1. Eine gerade Funktion ist punktsymmetrisch zum Ursprung.

Richtig
Falsch

2. Wenn f(2)=5 ist und f(-2)=5, dann ist der Graph achsensymmetrisch.

Richtig
Falsch

3. Die Funktion f(x)=x2+x+2 ist gerade.

Richtig
Falsch

4. Die Funktion f(x)=x3-1 ist ungerade.

Richtig
Falsch

5. Eine Zahl ohne Variable x ist gerade.

Richtig
Falsch

Punkte: 0 / 0


Weiter zum Kapitel Grenzwerte im Unendlichen


Zurück zur Übersicht
Von „http://rmg.zum.de/index.php?title=Facharbeit_Florian_Wilk/Symmetrie_von_Funktionsgraphen&oldid=27827“