Strecken und Spiegeln von Funktionsgraphen: Unterschied zwischen den Versionen
(→Spiegelung an der y-Achse) |
(→Beispielaufgaben) |
||
| Zeile 164: | Zeile 164: | ||
== <span style="color: blue">Beispielaufgaben</span> == | == <span style="color: blue">Beispielaufgaben</span> == | ||
| − | ''' <span style="color: blue">Aufgabe 1:</span>''' <br /> | + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 1:</span>''' <br /> |
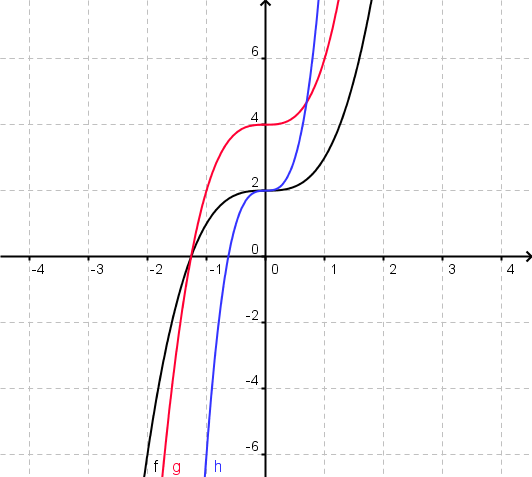
| − | Zeichne in ein gemeinsames Koordinatensystem die Funktion f(x)=x<sup>3</sup>+2, sowie die Funktionen g(x)=2f(x) und h(x)=f(2x). <br /> <br /> | + | Zeichne in ein gemeinsames Koordinatensystem die Funktion f(x)=x<sup>3</sup>+2, sowie die Funktionen g(x)=2f(x) und h(x)=f(2x) (handschriftlich). <br /> <br /> |
<popup name="Lösung"> | <popup name="Lösung"> | ||
[[Bild:Lösung Strekungsaufgabe 2.1.png|600px]] | [[Bild:Lösung Strekungsaufgabe 2.1.png|600px]] | ||
| − | </popup> <br /> | + | </popup> </div> <br /> |
| − | ''' <span style="color: blue">Aufgabe 2:</span>''' <br /> | + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 2:</span>''' <br /> |
Gegeben ist die Funktion f(x)=2x<sup>3</sup>-x<sup>2</sup>+2x+1. Erstelle jeweils die neuen Funktionen nach den folgenden Anweisungen. Verwende zum Weiterrechnen jeweils den vorangegangenen Funktionsterm.<br /> | Gegeben ist die Funktion f(x)=2x<sup>3</sup>-x<sup>2</sup>+2x+1. Erstelle jeweils die neuen Funktionen nach den folgenden Anweisungen. Verwende zum Weiterrechnen jeweils den vorangegangenen Funktionsterm.<br /> | ||
:a) Streckung um den Faktor 3 in y-Richtung <br /> | :a) Streckung um den Faktor 3 in y-Richtung <br /> | ||
| Zeile 204: | Zeile 204: | ||
::l(x)=-12(-x<sup>3</sup> )+3(-x<sup>2</sup> )-3(-x)-0,75 <br /> | ::l(x)=-12(-x<sup>3</sup> )+3(-x<sup>2</sup> )-3(-x)-0,75 <br /> | ||
::l(x)=12x<sup>3</sup>-3x<sup>2</sup>+3x-0,75 <br /> <br /> | ::l(x)=12x<sup>3</sup>-3x<sup>2</sup>+3x-0,75 <br /> <br /> | ||
| − | </popup> | + | </popup> </div> |
| − | ''' <span style="color: blue">Aufgabe 3:</span>''' <br /> | + | <div style="margin:0px; margin-right:90px; border: solid thin green; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; ">''' <span style="color: blue">Aufgabe 3:</span>''' <br /> |
Finde die passenden Paare. <br /> | Finde die passenden Paare. <br /> | ||
<div class="memo-quiz"> | <div class="memo-quiz"> | ||
| Zeile 222: | Zeile 222: | ||
|} | |} | ||
| − | </div> <br /> | + | </div> </div> <br /> |
|} | |} | ||
Version vom 23. Januar 2010, 21:58 Uhr
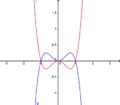
Strecken und Spiegeln von FunktionsgraphenStreckung in y-Richtung
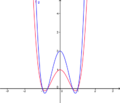
Streckung in x-Richtung Problemstellung:
Spiegelung an der x-AchseBisher haben wir das Verhalten der Funktionsgraphen nur für positive Werte von k untersucht. Nun soll k den Wert -1 annehmen. Aus den oben erstellten
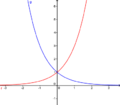
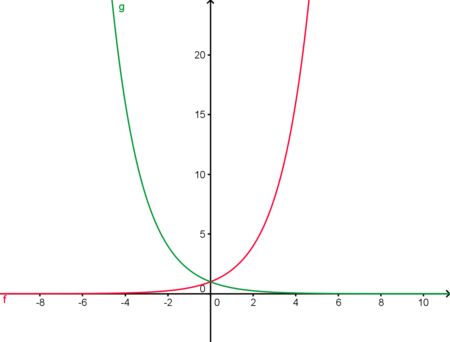
Spiegelung an der y-AchseNun betrachten wir den Fall g(x)=f(-x) am Beispiel f(x)=2x.
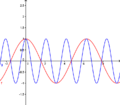
Wie sich der Graph einer Funktion verhält, wenn er an der x-Achse gespiegelt und dann in y-Richtung gestreckt wird, kannst du im untenstehenden Applet beobachten.
Beispielaufgaben Aufgabe 1: Zeichne in ein gemeinsames Koordinatensystem die Funktion f(x)=x3+2, sowie die Funktionen g(x)=2f(x) und h(x)=f(2x) (handschriftlich). Aufgabe 2:
Gegeben ist die Funktion f(x)=2x3-x2+2x+1. Erstelle jeweils die neuen Funktionen nach den folgenden Anweisungen. Verwende zum Weiterrechnen jeweils den vorangegangenen Funktionsterm.
Aufgabe 3: Finde die passenden Paare. |
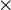 f(x). Dadurch nimmt g bei einem Koeffizienten k>1 einen größeren Funktionswert an als der Graph von f. Der Graph ist also in y-Richtung gestreckt. Dasselbe gilt auch für 0<k<1, nur dass der Graph g hier kleinere Funktionswerte annimmt. Die Nullstellen bleiben dabei unverändert!
f(x). Dadurch nimmt g bei einem Koeffizienten k>1 einen größeren Funktionswert an als der Graph von f. Der Graph ist also in y-Richtung gestreckt. Dasselbe gilt auch für 0<k<1, nur dass der Graph g hier kleinere Funktionswerte annimmt. Die Nullstellen bleiben dabei unverändert!
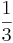 x)=cos
x)=cos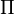 )=-1
)=-1 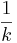 x)
x) 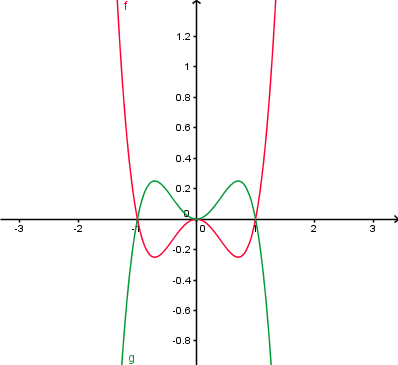
 =2
=2