Übungsaufgaben: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 135: | Zeile 135: | ||
'''3. Der Zusammenhang g(x)=f(-x) entspricht''' (!Einer Achsensymmetrie zur y-Achse) (!Einer Spiegelung an der x-Achse) (!Einer Punktsymmetrie zum Ursprung) (Einer Spiegelung an der y-Achse) (!Einer Streckung in x-Richtung) | '''3. Der Zusammenhang g(x)=f(-x) entspricht''' (!Einer Achsensymmetrie zur y-Achse) (!Einer Spiegelung an der x-Achse) (!Einer Punktsymmetrie zum Ursprung) (Einer Spiegelung an der y-Achse) (!Einer Streckung in x-Richtung) | ||
| − | '''4. Der abgebildete Graph der Funktion f(x)=x<sup>4</sup>-3x<sup>2</sup>+1 ist [[Bild: | + | '''4. Der abgebildete Graph der Funktion f(x)=x<sup>4</sup>-3x<sup>2</sup>+1 ist [[Bild: Abschlusstest2neu.png|300px]] ''' (!Punktsymmetrisch zum Ursprung) (Gerade) (Ganzrational) (!Quadratisch) (Achsensymmetrisch zur y-Achse) (!Ungerade) (Divergent) (!Konvergent) |
''' 5. Der Funktionsterm der Funktion g(x), die von f(x)=2x<sup>4</sup>-x<sup>3</sup> ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet''' (6x<sup>4</sup>-3x<sup>3</sup>+2) (!2[3x]<sup>4</sup>-[2x]<sup>3</sup>+2) (!6x<sup>4</sup>-3x<sup>3</sup>+6) (!5x<sup>4</sup>-3x<sup>3</sup>+1) (!6[x+2]<sup>4</sup>-3[x+2]<sup>3</sup>) (!6x<sup>4</sup>-3x<sup>3</sup>) | ''' 5. Der Funktionsterm der Funktion g(x), die von f(x)=2x<sup>4</sup>-x<sup>3</sup> ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet''' (6x<sup>4</sup>-3x<sup>3</sup>+2) (!2[3x]<sup>4</sup>-[2x]<sup>3</sup>+2) (!6x<sup>4</sup>-3x<sup>3</sup>+6) (!5x<sup>4</sup>-3x<sup>3</sup>+1) (!6[x+2]<sup>4</sup>-3[x+2]<sup>3</sup>) (!6x<sup>4</sup>-3x<sup>3</sup>) | ||
| Zeile 149: | Zeile 149: | ||
'''10. Um einen Graphen an der y-Achse zu spiegeln''' (!Multipliziert man den Funktionsterm mit -1) (Setzt man für f[x] f[-x]ein ) (Schreibt man vor jedes x ein „Minus“ ) (!Verschiebt man den Graphen nach rechts oder links [je nach Lage]) | '''10. Um einen Graphen an der y-Achse zu spiegeln''' (!Multipliziert man den Funktionsterm mit -1) (Setzt man für f[x] f[-x]ein ) (Schreibt man vor jedes x ein „Minus“ ) (!Verschiebt man den Graphen nach rechts oder links [je nach Lage]) | ||
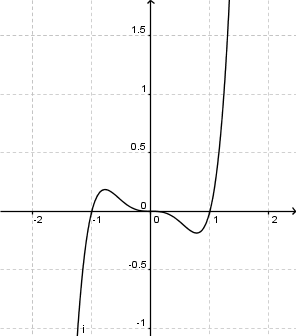
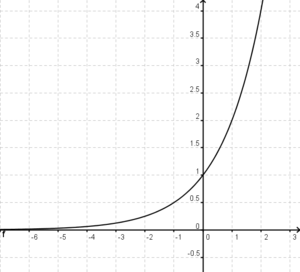
| − | '''11. Um was für eine Funktion handelt es sich? [[Bild: | + | '''11. Um was für eine Funktion handelt es sich? [[Bild: Abschlusstest1neu.png|300px]] ''' (Exponentialfunktion) (!Lineare Funktion ) (!Trigonometrische Funktion) (!Gebrochen rationale Funktion) |
'''12. <math>\lim_{x\to\infty} {sinx \over x}=</math>''' (!Existiert nicht) (!Unendlich) (0)(!1) | '''12. <math>\lim_{x\to\infty} {sinx \over x}=</math>''' (!Existiert nicht) (!Unendlich) (0)(!1) | ||
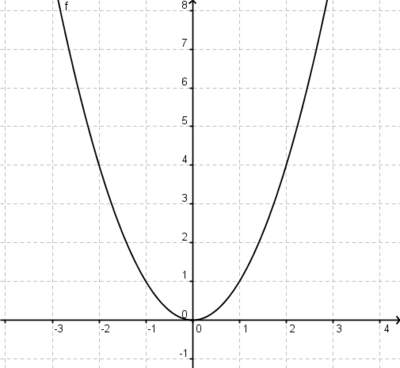
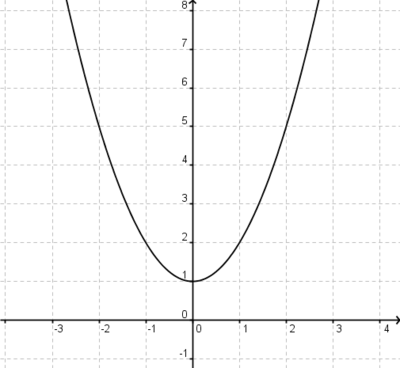

 Streckung um 0,5 in y-Richtung
Streckung um 0,5 in y-Richtung 
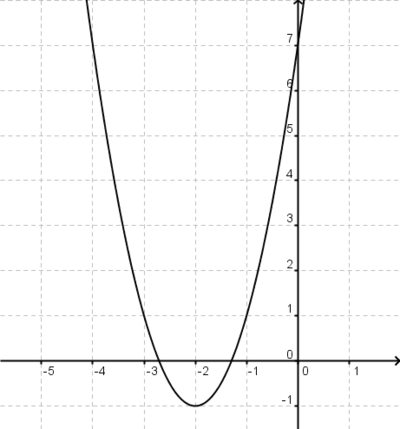
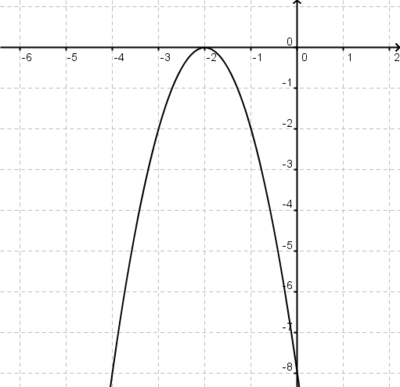


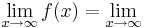 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=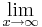 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=
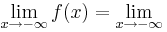 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=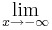 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=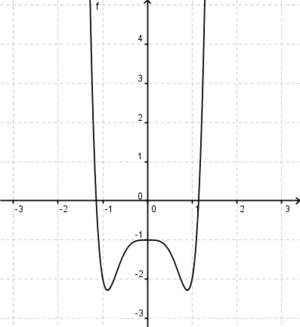
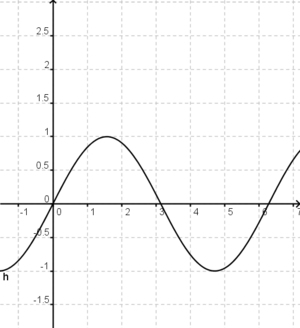







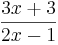 ist eine (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion)
ist eine (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion)
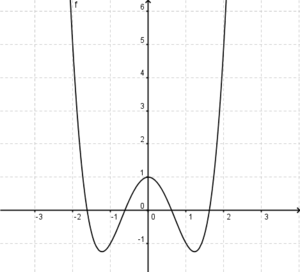
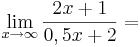 (!Unendlich) (!2) (!1) (!0) (4) (!-2) (!0,5)
(!Unendlich) (!2) (!1) (!0) (4) (!-2) (!0,5)
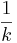 )
)
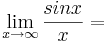 (!Existiert nicht) (!Unendlich) (0)(!1)
(!Existiert nicht) (!Unendlich) (0)(!1)

