Übungsaufgaben: Unterschied zwischen den Versionen
| Zeile 69: | Zeile 69: | ||
{| | {| | ||
|- | |- | ||
| − | | [[Bild:Aufgabe6.3. | + | | [[Bild:Aufgabe6.3.1neupng|300px]] || [[Bild:Aufgabe6.3.4neupng|300px]] || [[Bild:Aufgabe6.3.3neupng|300px]] || [[Bild:Aufgabe6.3.2neupng|300px]] |
|- | |- | ||
| <strong> Ganzrationale Funktion </strong> || <strong> Ganzrationale Funktion </strong> || <strong> Trigonometrische Funktion </strong> || <strong> Ganzrationale Funktion </strong> | | <strong> Ganzrationale Funktion </strong> || <strong> Ganzrationale Funktion </strong> || <strong> Trigonometrische Funktion </strong> || <strong> Ganzrationale Funktion </strong> | ||
Version vom 23. Januar 2010, 15:05 Uhr
Übungsaufgaben Aufgabe 1:
Aufgabe 4:
Aufgabe 6: Abschlusstest 1.Die Funktion f(x)= 2. Eine Funktion, die keinen Grenzwert besitzt, ist (Divergent) (!Konvergent) (!Punktsymmetrisch zum Ursprung) (!Gebrochen rational) 3. Der Zusammenhang g(x)=f(-x) entspricht (!Einer Achsensymmetrie zur y-Achse) (!Einer Spiegelung an der x-Achse) (!Einer Punktsymmetrie zum Ursprung) (Einer Spiegelung an der y-Achse) (!Einer Streckung in x-Richtung) 4. Der abgebildete Graph der Funktion f(x)=x4-3x2+1 ist 5. Der Funktionsterm der Funktion g(x), die von f(x)=2x4-x3 ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet (6x4-3x3+2) (!2[3x]4-[2x]3+2) (!6x4-3x3+6) (!5x4-3x3+1) (!6[x+2]4-3[x+2]3) (!6x4-3x3) 6. 7. Der Graph der Funktion f(x)=2x2+1 ist gegenüber dem Graphen g(x)=x2-1 (!In y-Richtung Gestreckt und nach unten verschoben) (Nach oben verschoben ) (In y-Richtung gestreckt und in positiver y-Richtung verschoben ) (In y-Richtung gestreckt ) (!In negativer y-Richtung verschoben) (!Gar nicht verschoben) (!Gar nicht gestreckt) 8. Was trifft auf diese Funktion zu? f(x)=sinx (Punktsymmetrie zum Ursprung) (Trigonometrisch) (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (Ungerade) (!Achsensymmetrie zur y-Achse) (f[0]=0) 9. Bei einer Streckung in x-Richtung (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert ) (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor 10. Um einen Graphen an der y-Achse zu spiegeln (!Multipliziert man den Funktionsterm mit -1) (Setzt man für f[x] f[-x]ein ) (Schreibt man vor jedes x ein „Minus“ ) (!Verschiebt man den Graphen nach rechts oder links [je nach Lage]) 11. Um was für eine Funktion handelt es sich? 12. 13. Wie lautet der Funktionsterm der Funktion g(x), die von f(x)=x3+x2-1 ausgehend zwei Einheiten weiter rechts verläuft? (![x+2]3+[x+2]2-1) (!x3+x2+1) ([x-2]3+[x-2]2-1) (!x3+x2-3) (x3-5x2+8x-5) (!x3+5x2-8x+5)
Du hast es geschafft! |
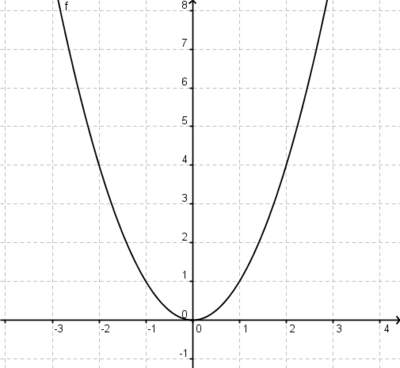
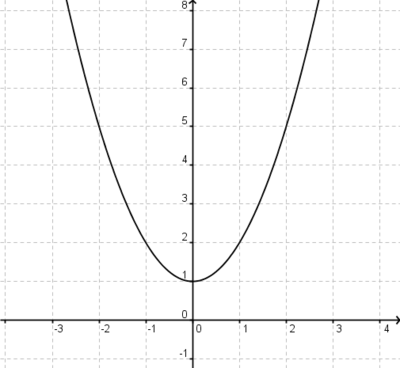

 Streckung um 0,5 in y-Richtung
Streckung um 0,5 in y-Richtung 
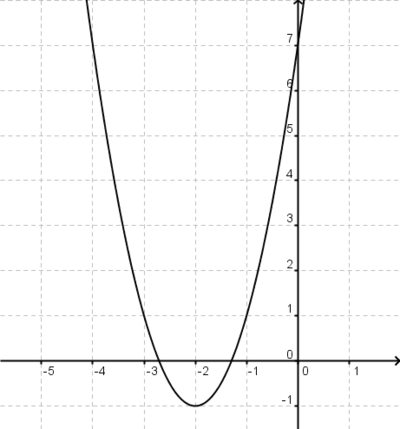
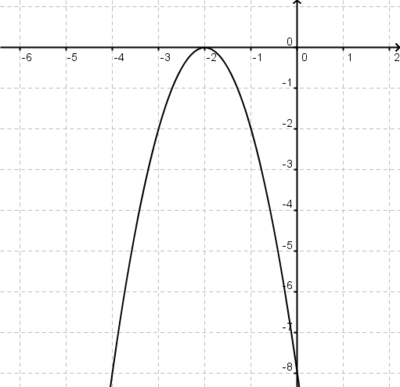


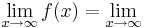 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=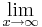 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=
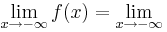 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=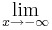 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=





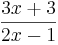 ist eine (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion)
ist eine (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion)

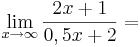 (!Unendlich) (!2) (!1) (!0) (4) (!-2) (!0,5)
(!Unendlich) (!2) (!1) (!0) (4) (!-2) (!0,5)
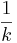 )
)

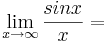 (!Existiert nicht) (!Unendlich) (0)(!1)
(!Existiert nicht) (!Unendlich) (0)(!1)

