Übungsaufgaben: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 127: | Zeile 127: | ||
<span style="color: blue">'''Aufgabe 6:''' Abschlusstest</span> <br /> | <span style="color: blue">'''Aufgabe 6:''' Abschlusstest</span> <br /> | ||
| − | Der folgende | + | Der folgende Multiple Choice Test ist die letzte Aufgabe des Lernpfades. Er deckt alle behandelten Themengebiete ab. Wenn du bei einigen Aufgaben nicht weiter weißt, kannst du deine Notizen zur Rate ziehen. Sollte auch das nicht helfen, solltest du dir die entsprechenden Kapitel noch einmal anschauen und deine Notizen eventuell überarbeiten. Wie immer können mehrere Antwortmöglichkeiten richtig sein. <br /> |
<div class="multiplechoice-quiz"> | <div class="multiplechoice-quiz"> | ||
'''1.Die Funktion f(x)=<math>{3x+3 \over2x-1}</math> ist eine''' (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion) | '''1.Die Funktion f(x)=<math>{3x+3 \over2x-1}</math> ist eine''' (!Lineare Funktion) (!Ganzrationale Funktion) (!Trigonometrische Funktion) (!Exponentialfunktion) (Gebrochen rationale Funktion) | ||
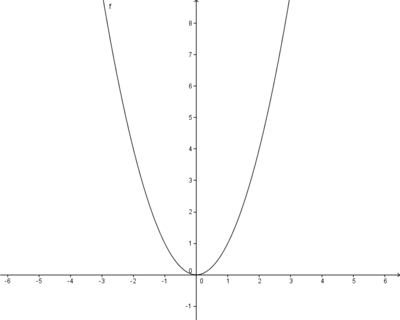
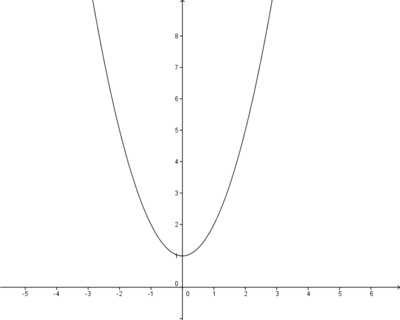
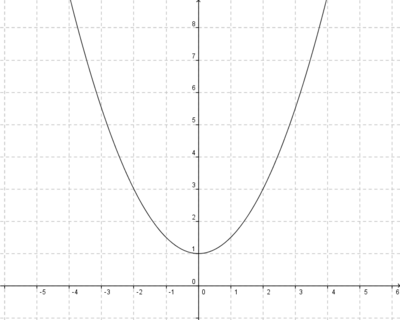
 Streckung um 0,5 in y-Richtung
Streckung um 0,5 in y-Richtung 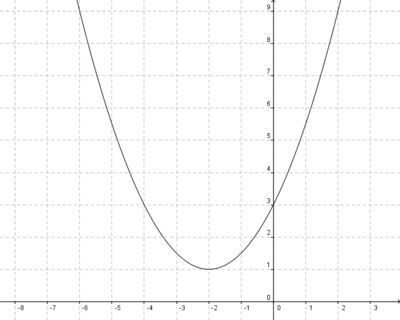
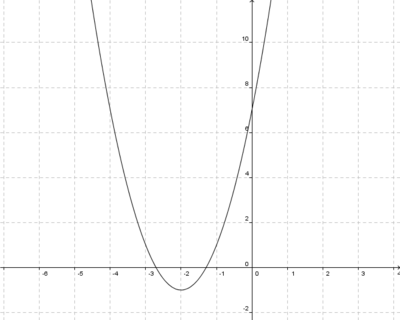
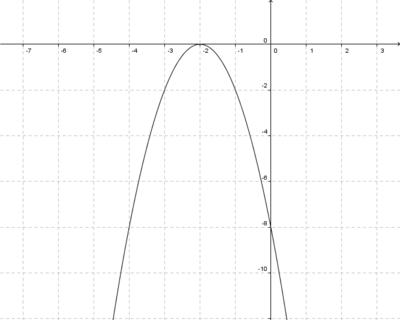

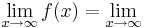 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=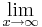 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=
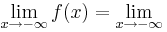 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=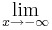 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=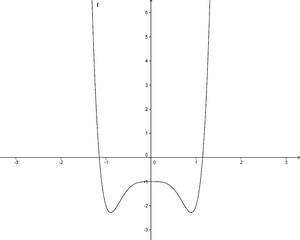
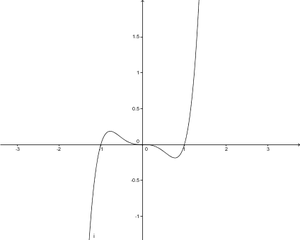
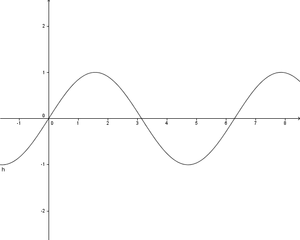






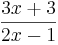 ist eine
ist eine