Übungsaufgaben: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 133: | Zeile 133: | ||
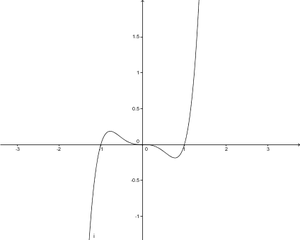
'''Der abgebildete Graph der Funktion f(x)=x<sup>4</sup>-3x<sup>2</sup>+1 ist''' (!Punktsymmetrisch zum Ursprung) (Gerade) (Ganzrational) (!Quadratisch) (Achsensymmetrisch zur y-Achse) (!Ungerade) (Divergent) (!Konvergent) | '''Der abgebildete Graph der Funktion f(x)=x<sup>4</sup>-3x<sup>2</sup>+1 ist''' (!Punktsymmetrisch zum Ursprung) (Gerade) (Ganzrational) (!Quadratisch) (Achsensymmetrisch zur y-Achse) (!Ungerade) (Divergent) (!Konvergent) | ||
| − | |||
| − | |||
''' Der Funktionsterm der Funktion g(x), die von f(x)=2x<sup>4</sup>-x<sup>3</sup> ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet''' (6x<sup>4</sup>-3x<sup>3</sup>+2) (!2[3x]<sup>4</sup>-[2x]<sup>3</sup>+2) (!6x<sup>4</sup>-3x<sup>3</sup>+6) (!5x<sup>4</sup>-3x<sup>3</sup>+1) (!6[x+2]<sup>4</sup>-3[x+2]<sup>3</sup>) (!6x<sup>4</sup>-3x<sup>3</sup>) | ''' Der Funktionsterm der Funktion g(x), die von f(x)=2x<sup>4</sup>-x<sup>3</sup> ausgehend um den Faktor 3 in y-Richtung getreckt und anschließend um 2 Einheiten nach oben verschoben wird, lautet''' (6x<sup>4</sup>-3x<sup>3</sup>+2) (!2[3x]<sup>4</sup>-[2x]<sup>3</sup>+2) (!6x<sup>4</sup>-3x<sup>3</sup>+6) (!5x<sup>4</sup>-3x<sup>3</sup>+1) (!6[x+2]<sup>4</sup>-3[x+2]<sup>3</sup>) (!6x<sup>4</sup>-3x<sup>3</sup>) | ||
| Zeile 143: | Zeile 141: | ||
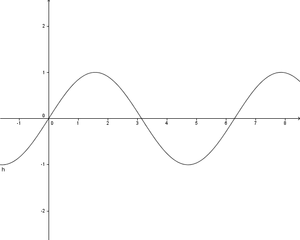
''' Was trifft auf diese Funktion zu? f(x)=sinx''' (Punktsymmetrie zum Ursprung) (Trigonometrisch) (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (Ungerade) (!Achsensymmetrie zur y-Achse) (!f[0]=0) | ''' Was trifft auf diese Funktion zu? f(x)=sinx''' (Punktsymmetrie zum Ursprung) (Trigonometrisch) (!Linear) (!Graph: Parabel) (!Keine Nullstellen) (Ungerade) (!Achsensymmetrie zur y-Achse) (!f[0]=0) | ||
| − | |||
| − | |||
''' Bei einer Streckung in x-Richtung ''' (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert ) (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor {1 \over k}) | ''' Bei einer Streckung in x-Richtung ''' (!Verändert sich die Amplitude einer trigonometrischen Funktion) (Bleiben die Funktionswerte an der Stelle x=0 unverändert ) (!Bleiben die Nullstellen unverändert) (!Wird der Graph an der x-Achse gespiegelt) (Erfolgt die Streckung um den Faktor {1 \over k}) | ||
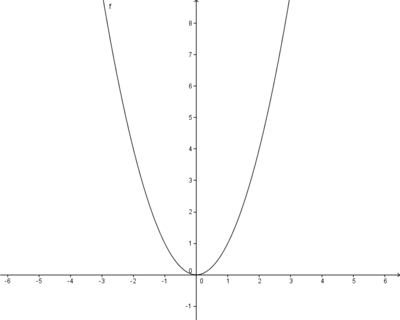
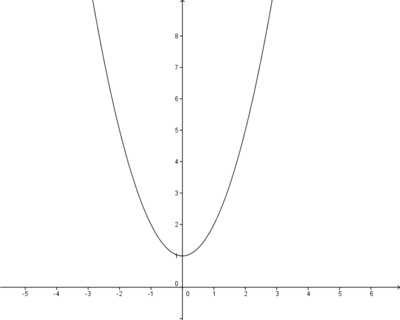
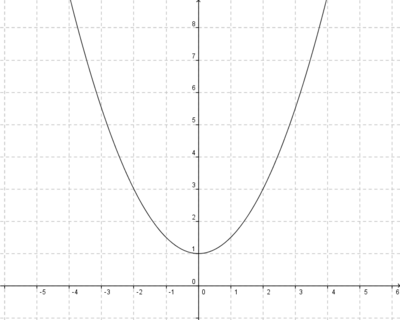
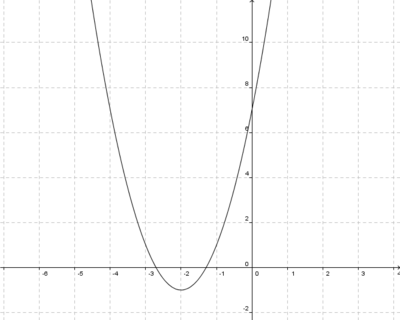
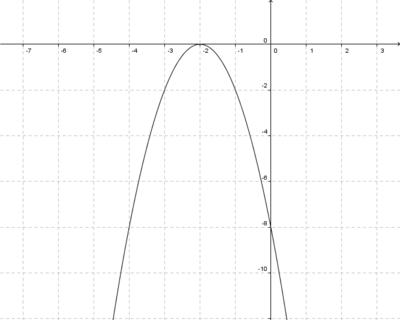
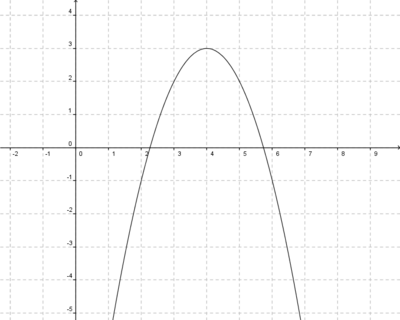
 Streckung um 0,5 in y-Richtung
Streckung um 0,5 in y-Richtung 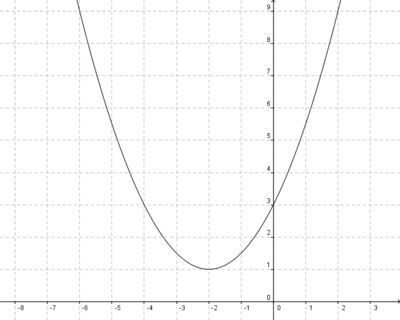

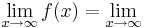 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=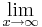 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=
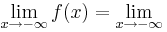 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=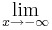 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=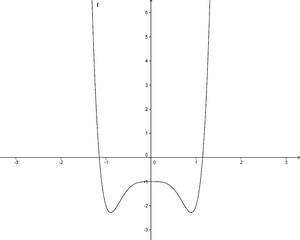






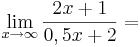 (!Unendlich) (!2) (!1) (!0) (4) (!-2) (0,5)
(!Unendlich) (!2) (!1) (!0) (4) (!-2) (0,5)
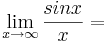 (!Existiert nicht) (!Unendlich) (0)(!1)
(!Existiert nicht) (!Unendlich) (0)(!1)

