Strecken und Spiegeln von Funktionsgraphen: Unterschied zwischen den Versionen
(→Spiegelung an der x-Achse) |
|||
| Zeile 101: | Zeile 101: | ||
g(x)= -1k×f(x) und g(x)=f(-1kx), also g(x)= -f(x) und g(x)=f(-x). <br /> | g(x)= -1k×f(x) und g(x)=f(-1kx), also g(x)= -f(x) und g(x)=f(-x). <br /> | ||
Zunächst betrachten wir den Fall g(x)= -f(x). <br /> | Zunächst betrachten wir den Fall g(x)= -f(x). <br /> | ||
| + | |||
| + | {| | ||
| + | ! width="490" | | ||
| + | ! width="20" | | ||
| + | ! width="400" | | ||
| + | |- | ||
| + | | valign="top" | | ||
[[Bild:Spiegelung an der x-Achse.png|450px|left]] | [[Bild:Spiegelung an der x-Achse.png|450px|left]] | ||
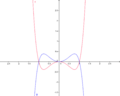
| − | Im nebenstehenden Koordinatensystem ist der Graph von f mit dem Funktionsterm f(x)=x<sup>4</sup>-x<sup>2</sup> rot dargestellt. Um die Funktionswerte des grün dargestellten Graphen von g zu erhalten, werden die Funktionswerte von f(x) mit k=-1 multipliziert. Wie in der Abbildung zu erkennen ist, handelt es sich beim Graphen von g um eine Spiegelung an der x-Achse. <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | + | |
| + | | | ||
| + | | valign="top" | | ||
| + | <br /> <br /> <br /> Im nebenstehenden Koordinatensystem ist der Graph von f mit dem Funktionsterm f(x)=x<sup>4</sup>-x<sup>2</sup> rot dargestellt. Um die Funktionswerte des grün dargestellten Graphen von g zu erhalten, werden die Funktionswerte von f(x) mit k=-1 multipliziert. Wie in der Abbildung zu erkennen ist, handelt es sich beim Graphen von g um eine Spiegelung an der x-Achse. <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> | ||
| + | |||
| + | |} | ||
== <span style="color: blue">Spiegelung an der y-Achse</span> == | == <span style="color: blue">Spiegelung an der y-Achse</span> == | ||
Version vom 18. Januar 2010, 21:10 Uhr
Inhaltsverzeichnis |
Strecken und Spiegeln von Funktionsgraphen
Streckung in y-Richtung
|
Zur Erinnerung: |
|
Problemstellung: |
|
Erklärung: |
|
Beispiel:
|
Streckung in x-Richtung
Problemstellung:
|
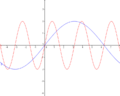
Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=cosx eingezeichnet. Durch eine Streckung in x-Richtung um den Faktor 3 entsteht der Graph g. Wie lautet der Funktionsterm von g? |
|
Erklärung: |
|
Beispiel:
|
|
Ist der Streckungsfaktor 0<k<1, z.B. k=0,5, dann entspricht der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle 0,5. |
|
Merke:
Besteht zwischen zwei Funktionen der Zusammenhang g(x)=k×f(x) mit k>0, dann ist der Graph von g gegenüber dem von f in y-Richtung um den Faktor k gestreckt. Besteht zwischen zwei Funktionen der Zusammenhang g(x)=f(kx) mit k>0, dann ist der Graph von g gegenüber dem von f um den Faktor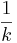 in x-Richtung gestreckt. in x-Richtung gestreckt. |
Spiegelung an der x-Achse
Bisher haben wir das Verhalten der Funktionsgraphen nur für positive Werte von k untersucht. Nun soll k den Wert -1 annehmen. Aus den oben erstellten Formeln ergeben sich nun die Fälle
g(x)= -1k×f(x) und g(x)=f(-1kx), also g(x)= -f(x) und g(x)=f(-x).
Zunächst betrachten wir den Fall g(x)= -f(x).
|
|
Spiegelung an der y-Achse
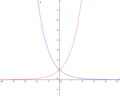
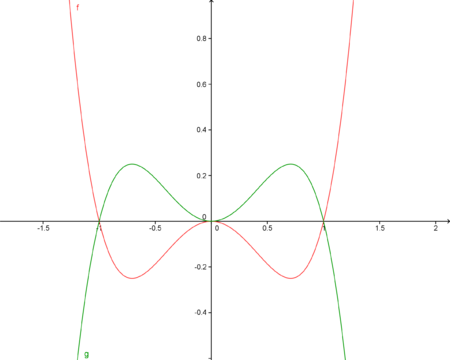
Nun betrachten wir den Fall g(x)=f(-x) am Beispiel f(x)=2x.
Im nebenstehenden Koordinatensystem ist der Graph von f rot dargestellt. Für den Graphen von g (grün dargestellt) gilt der Funktionsterm g(x)=2-x. Betrachtet man die beiden Graphen zusammen, so fällt auf, dass der Graph von g aus einer Spiegelung von f an der y-Achse entsteht.
Der Graph von g mit g(x)= -f(x) geht aus dem Graphen von f durch eine Spiegelung an der x-Achse hervor.
Der Graph von g mit g(x)=f(-x) geht aus dem Graphen von f durch eine Spiegelung an der y-Achse hervor.
Beispielaufgaben
Aufgabe 1:
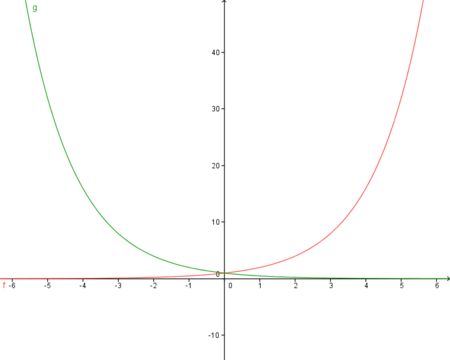
Zeichne in ein gemeinsames Koordinatensystem die Funktion f(x)=x3+2, sowie die Funktionen g(x)=2f(x) und h(x)=f(2x).
Aufgabe 2:
Gegeben ist die Funktion f(x)=2x3-x2+2x+1. Erstelle jeweils die neuen Funktionen nach den folgenden Anweisungen. Verwende zum Weiterrechnen jeweils den vorangegangenen Funktionsterm.
- a) Streckung um den Faktor 3 in y-Richtung
- b) Spiegelung an der x-Achse
- c) Streckung um den Faktor 0,5 in x-Richtung
- d) Streckung um den Faktor 0,25 in y-Richtung
- e) Spiegelung an der y-Achse
Aufgabe 3:
Finde die passenden Paare.
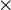 k
k 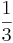 x)=cos
x)=cos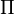 )=-1
)=-1 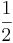
 =2
=2