Strecken und Spiegeln von Funktionsgraphen: Unterschied zwischen den Versionen
(→Streckung in y-Richtung) |
|||
| Zeile 45: | Zeile 45: | ||
== <span style="color: blue">Streckung in x-Richtung</span> == | == <span style="color: blue">Streckung in x-Richtung</span> == | ||
| − | ''' <span style="color: blue">Problemstellung:</span>''' | + | ''' <span style="color: blue">Problemstellung:</span>''' <br /> |
| − | + | {| | |
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
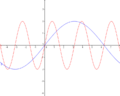
Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=cosx eingezeichnet. Durch eine Streckung in x-Richtung um den Faktor 3 entsteht der Graph g. Wie lautet der Funktionsterm von g? | Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=cosx eingezeichnet. Durch eine Streckung in x-Richtung um den Faktor 3 entsteht der Graph g. Wie lautet der Funktionsterm von g? | ||
| + | |} <br /> | ||
| + | <ggb_applet width="892" height="512" version="3.2" ggbBase64="UEsDBBQACAAIACmOMjwAAAAAAAAAAAAAAAAMAAAAZ2VvZ2VicmEueG1stVbfb9MwEH5mf4WVp4FE2zS026RkEwxNmjTgoTAk3pzkmpg6duQfXbq/nrOd9BcgDRhPtu8u5++++3xtetU1nKxBaSZFFsWjSURAFLJkosoia5avz6Ory5O0AllBrihZStVQk0XJaBo5u2WXJy9SXcsHQrkPuWfwkEVGWYiIbhXQUtcAJpiXlGu0U9sxzqjafMq/Q2H0zhFy3IrWmiFJ0ZR3TA/Hsb+v5cy8Z2tWgiJcFlk0nyFy3N2DMqygPIveTIJlmkXTIyeaEuetpWKPUhgXvku+RAshmj0CEjJ1tnTs60zBFpyVjApXjMeBQYQ8sNLUCCGZY0pgVY1YZ/EkZCukVOViow00pPsGSmLS+NzxvAmn6XniThpx4YWziXf1p3gSj2bJxdmbBKOS+VkccsJ6AcZgizShHeiBqEqxcn9/q99JXm65bSUT5pq2xirf3aQ3LczG3YXXKof9rag49LYY2a+hWOWyWwQ+kpD686b1n3g4eXUtuVREOaZnGNCveVh9jMO5jZr4mImP6HO4pFt/fDH1EX7Nw+qjOBMBWl93PBQ9sE07pokzOEZRlAMdnOaATY6IFczcDQcUw2pXqYv/aJscH8O+HLYp42dKmY6PdJSuQAngQS0C+2ql1WTtVBla53GUULAGj8HRE0Jds74ggGAtoVIw4A5PKdDlvQeKPDKn4wGEw6ARa2FwJGA9xtWyMAplYEVF1mi8sWLlvLpStK1BuAdt8DFl0Q12EOsiXxlfRaSkBr91cwI6nATaDZnAG8HScNJ0La6n3UuSkUJq3HgowKEBfIPGi2xphYeyZXwZHUrB1Mi5wOyOlf6jvlQ/l6SfMUdt2/UX3b8RJk6jtqa4G/XpON3gvNnn0mf7IMtDhqnATnn68Nm3LoHTQgsQVDRAJC0m9E9xr81PqAsFFBj6iSthG1Cs2Fa58lQhNNsDTEbPzEz8RGb6OM39yG6YCLSShnbu9botzbXk1sCiQA2LO1l4Cgd0/ZCNJz4WP0qmcz8qcWZeuM2SdbAbdr8e7U8Szd9376AxR4rPoqoXfBUEvzxdkVcEJU+eoPnq/2l+GNn/rPo/VO54f87439j+P8blD1BLBwh3ZPlhNwMAAJUIAABQSwECFAAUAAgACAApjjI8d2T5YTcDAACVCAAADAAAAAAAAAAAAAAAAAAAAAAAZ2VvZ2VicmEueG1sUEsFBgAAAAABAAEAOgAAAHEDAAAAAA==" framePossible = "false" showResetIcon = "false" showAnimationButton = "true" enableRightClick = "false" errorDialogsActive = "true" enableLabelDrags = "false" showMenuBar = "false" showToolBar = "false" showToolBarHelp = "false" showAlgebraInput = "false" /> <br /> <br /> | ||
| − | ''' <span style="color: blue">Erklärung:</span>''' Eine Streckung um den Faktor 3 in x-Richtung bedeutet, dass der Graph von g den Funktionswert, den der Graph von f an der Stelle x annimmt, erst an der Stelle 3x annimmt. <br /> | + | {| |
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
| + | ''' <span style="color: blue">Erklärung:</span>''' <br /> | ||
| + | Eine Streckung um den Faktor 3 in x-Richtung bedeutet, dass der Graph von g den Funktionswert, den der Graph von f an der Stelle x annimmt, erst an der Stelle 3x annimmt. <br /> | ||
Es entsteht also der Zusammenhang f(x)=g(3x) oder g(x)=f(<math>{1 \over 3}</math>x)=cos<math>{1 \over 3}</math>x <br /> | Es entsteht also der Zusammenhang f(x)=g(3x) oder g(x)=f(<math>{1 \over 3}</math>x)=cos<math>{1 \over 3}</math>x <br /> | ||
| − | (Allgemein: f(x)=g(kx) oder g(x)=f(<math>{1 \over k}</math>x)) <br /> <br /> <br /> | + | (Allgemein: f(x)=g(kx) oder g(x)=f(<math>{1 \over k}</math>x)) |
| + | |} <br /> <br /> <br /> | ||
| + | {| | ||
| + | ! width="940" | | ||
| + | |- | ||
| + | | valign="top" | | ||
<div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> ''' <span style="color: blue">Beispiel:</span>''' <br /> | <div style="margin:0px; margin-right:90px; border: solid blue; padding: 1em 1em 1em 1em; background-color:white; width:90%; align:center; "> ''' <span style="color: blue">Beispiel:</span>''' <br /> | ||
:k=2 <br /> | :k=2 <br /> | ||
| Zeile 59: | Zeile 74: | ||
::g(<math>\Pi</math>)=f(<math>{1 \over 2}</math><math>\Pi</math>) <br /> | ::g(<math>\Pi</math>)=f(<math>{1 \over 2}</math><math>\Pi</math>) <br /> | ||
::g(<math>\Pi</math>)=0 | ::g(<math>\Pi</math>)=0 | ||
| − | </div> <br /> <br /> | + | </div> |
| + | |} <br /> <br /> | ||
| + | {| | ||
| + | ! width="910" | | ||
| + | |- | ||
| + | | valign="top" | | ||
Ist der Streckungsfaktor 0<k<1, z.B. k=0,5, dann entspricht der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle 0,5. <br /> | Ist der Streckungsfaktor 0<k<1, z.B. k=0,5, dann entspricht der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle 0,5. <br /> | ||
Der Zusammenhang lautet also f(x)=g(0,5x) oder g(x)=f(2x). Das Verhalten des Graphen kannst du beobachten, wenn du im oben abgebildeten Koordinatensystem den Regler k verschiebst. | Der Zusammenhang lautet also f(x)=g(0,5x) oder g(x)=f(2x). Das Verhalten des Graphen kannst du beobachten, wenn du im oben abgebildeten Koordinatensystem den Regler k verschiebst. | ||
'''Der Funktionswert an der Stelle x=0 bleibt immer gleich.''' <br /> | '''Der Funktionswert an der Stelle x=0 bleibt immer gleich.''' <br /> | ||
Allgemein: g(x)=f(kx) mit dem Streckungsfaktor <math>{1 \over k}</math> | Allgemein: g(x)=f(kx) mit dem Streckungsfaktor <math>{1 \over k}</math> | ||
| − | <br /> <br /> | + | |} <br /> <br /> |
| + | |||
| + | {| | ||
| + | ! width="940" | | ||
| + | |- | ||
| + | | valign="top" | | ||
<div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "> ''' <span style="color: red">Merke:</span>''' | <div style="margin:0px; margin-right:90px; border: solid red; padding: 1em 1em 1em 1em; background-color:yellow; width:90%; align:center; "> ''' <span style="color: red">Merke:</span>''' | ||
Besteht zwischen zwei Funktionen der Zusammenhang g(x)=k×f(x) mit k>0, dann ist der Graph von g gegenüber dem von f in y-Richtung um den Faktor k gestreckt. | Besteht zwischen zwei Funktionen der Zusammenhang g(x)=k×f(x) mit k>0, dann ist der Graph von g gegenüber dem von f in y-Richtung um den Faktor k gestreckt. | ||
| − | Besteht zwischen zwei Funktionen der Zusammenhang g(x)=f(kx) mit k>0, dann ist der Graph von g gegenüber dem von f um den Faktor <math>{1 \over k}</math> in x-Richtung gestreckt.</div> <br /> <br /> | + | Besteht zwischen zwei Funktionen der Zusammenhang g(x)=f(kx) mit k>0, dann ist der Graph von g gegenüber dem von f um den Faktor <math>{1 \over k}</math> in x-Richtung gestreckt.</div> |
| + | |} <br /> <br /> | ||
== <span style="color: blue">Spiegelung an der x-Achse</span> == | == <span style="color: blue">Spiegelung an der x-Achse</span> == | ||
Version vom 18. Januar 2010, 19:43 Uhr
Inhaltsverzeichnis |
Strecken und Spiegeln von Funktionsgraphen
Streckung in y-Richtung
|
Zur Erinnerung: |
|
Problemstellung: |
|
Erklärung: |
|
Beispiel:
|
Streckung in x-Richtung
Problemstellung:
|
Im nebenstehenden Koordinatensystem ist der Graph der Funktion f(x)=cosx eingezeichnet. Durch eine Streckung in x-Richtung um den Faktor 3 entsteht der Graph g. Wie lautet der Funktionsterm von g? |
|
Erklärung: |
|
Beispiel:
|
|
Ist der Streckungsfaktor 0<k<1, z.B. k=0,5, dann entspricht der Funktionswert von f an der Stelle x dem Funktionswert von g an der Stelle 0,5. |
|
Merke:
Besteht zwischen zwei Funktionen der Zusammenhang g(x)=k×f(x) mit k>0, dann ist der Graph von g gegenüber dem von f in y-Richtung um den Faktor k gestreckt. Besteht zwischen zwei Funktionen der Zusammenhang g(x)=f(kx) mit k>0, dann ist der Graph von g gegenüber dem von f um den Faktor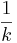 in x-Richtung gestreckt. in x-Richtung gestreckt. |
Spiegelung an der x-Achse
Bisher haben wir das Verhalten der Funktionsgraphen nur für positive Werte von k untersucht. Nun soll k den Wert -1 annehmen. Aus den oben erstellten Formeln ergeben sich nun die Fälle
g(x)= -1k×f(x) und g(x)=f(-1kx), also g(x)= -f(x) und g(x)=f(-x).
Zunächst betrachten wir den Fall g(x)= -f(x).
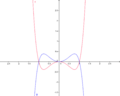
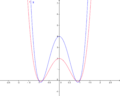
Im nebenstehenden Koordinatensystem ist der Graph von f mit dem Funktionsterm f(x)=x4-x2 rot dargestellt. Um die Funktionswerte des grün dargestellten Graphen von g zu erhalten, werden die Funktionswerte von f(x) mit k=-1 multipliziert. Wie in der Abbildung zu erkennen ist, handelt es sich beim Graphen von g um eine Spiegelung an der x-Achse.
Spiegelung an der y-Achse
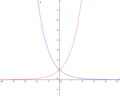
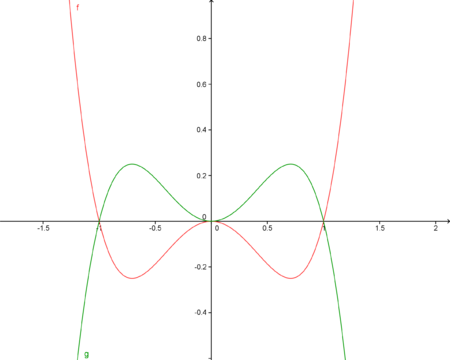
Nun betrachten wir den Fall g(x)=f(-x) am Beispiel f(x)=2x.
Im nebenstehenden Koordinatensystem ist der Graph von f rot dargestellt. Für den Graphen von g (grün dargestellt) gilt der Funktionsterm g(x)=2-x. Betrachtet man die beiden Graphen zusammen, so fällt auf, dass der Graph von g aus einer Spiegelung von f an der y-Achse entsteht.
Der Graph von g mit g(x)= -f(x) geht aus dem Graphen von f durch eine Spiegelung an der x-Achse hervor.
Der Graph von g mit g(x)=f(-x) geht aus dem Graphen von f durch eine Spiegelung an der y-Achse hervor.
Beispielaufgaben
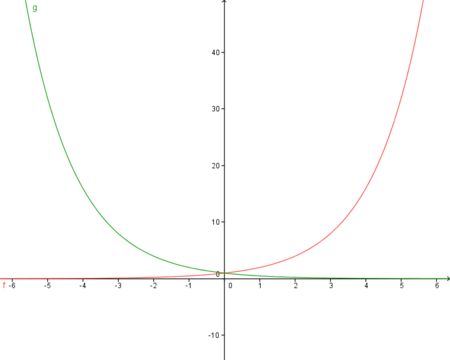
Aufgabe 1:
Zeichne in ein gemeinsames Koordinatensystem die Funktion f(x)=x3+2, sowie die Funktionen g(x)=2f(x) und h(x)=f(2x).
Aufgabe 2:
Gegeben ist die Funktion f(x)=2x3-x2+2x+1. Erstelle jeweils die neuen Funktionen nach den folgenden Anweisungen. Verwende zum Weiterrechnen jeweils den vorangegangenen Funktionsterm.
- a) Streckung um den Faktor 3 in y-Richtung
- b) Spiegelung an der x-Achse
- c) Streckung um den Faktor 0,5 in x-Richtung
- d) Streckung um den Faktor 0,25 in y-Richtung
- e) Spiegelung an der y-Achse
Aufgabe 3:
Finde die passenden Paare.
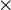 k
k 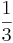 x)=cos
x)=cos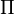 )=-1
)=-1 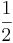
 =2
=2