Übungsaufgaben: Unterschied zwischen den Versionen
| Zeile 33: | Zeile 33: | ||
a) Bestimme die Definitionsmenge <br /> | a) Bestimme die Definitionsmenge <br /> | ||
b) Berechne die Nullstellen <br /> | b) Berechne die Nullstellen <br /> | ||
| − | c) Bestimme das Verhalten der Funktion an den Rändern des Definitionsbereichs <br /> | + | c) Bestimme das Verhalten der Funktion an den Rändern des Definitionsbereichs <br /> <br /> |
<popup name="Lösung"> | <popup name="Lösung"> | ||
| − | a) D=<math>\mathbb{R}</math> <br /> | + | a) <br /> D=<math>\mathbb{R}</math> <br /> |
| − | b) f(x)=4x<sup>6</sup>+8x<sup>5</sup>-12x<sup>4</sup>-24x<sup>3</sup> | + | b) <br /> f(x)=4x<sup>6</sup>+8x<sup>5</sup>-12x<sup>4</sup>-24x<sup>3</sup> |
| − | + | f(x)=4x<sup>3</sup>(x<sup>3</sup>+2x<sup>2</sup>-3x-6) <math>\rightarrow</math> x<sub>1</sub>=0 (dreifache Nullstelle) | |
| − | + | ||
| + | Ausprobieren: f(-2)=0 <math>\rightarrow</math> x<sub>2</sub>=-2 <br /> | ||
Polynomdivision: (x<sup>3</sup>+2x<sup>2</sup>-3x-6)÷(x+2)=x<sup>2</sup>-3 <math>\rightarrow</math> | Polynomdivision: (x<sup>3</sup>+2x<sup>2</sup>-3x-6)÷(x+2)=x<sup>2</sup>-3 <math>\rightarrow</math> | ||
x<sub>3</sub>=±√3 <br /> | x<sub>3</sub>=±√3 <br /> | ||
| − | c)<math>\lim_{x\to\infty} f(x)=\lim_{x\to\infty}</math>4x<sup>6</sup>+8x<sup>5</sup>-12x<sup>4</sup>-24x<sup>3</sup>=<math>\lim_{x\to\infty}</math>4x<sup>3</sup>(x<sup>3</sup>+2x<sup>2</sup>-3x-6)=<math>\infty</math> | + | c)<br /> <math>\lim_{x\to\infty} f(x)=\lim_{x\to\infty}</math>4x<sup>6</sup>+8x<sup>5</sup>-12x<sup>4</sup>-24x<sup>3</sup>=<math>\lim_{x\to\infty}</math>4x<sup>3</sup>(x<sup>3</sup>+2x<sup>2</sup>-3x-6)=<math>\infty</math> <br /> |
| + | <math>\lim_{x\to-\infty} f(x)=\lim_{x\to-\infty}</math>4x<sup>6</sup>+8x<sup>5</sup>-12x<sup>4</sup>-24x<sup>3</sup>=<math>\lim_{x\to-\infty}</math>4x<sup>3</sup>(x<sup>3</sup>+2x<sup>2</sup>-3x-6)=<math>\infty</math> | ||
</popup> | </popup> | ||
| + | <br /> <br /> | ||
'''Aufgabe 3:''' <br /> <br /> | '''Aufgabe 3:''' <br /> <br /> | ||
Version vom 15. Januar 2010, 16:35 Uhr
Übungsaufgaben
Aufgabe 1:
Beschreibe, wie die unten abgebildeten Funktionen aus den vorangegangen Funktionen entstanden sind.
Ausgangsfunktion
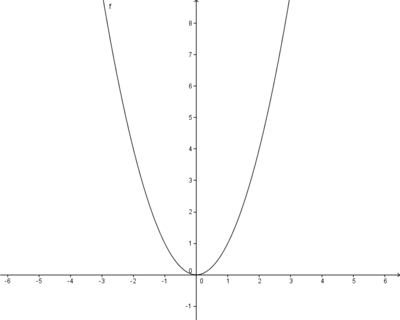
Beispiel:
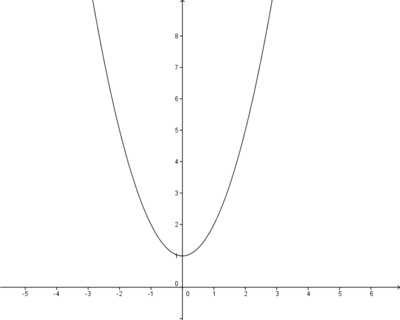
Verschiebung um 1 Einheit in positiver y-Richtung
Diese Funktion dient nun als Ausgangsfunktion für die nächste Funktion
a)
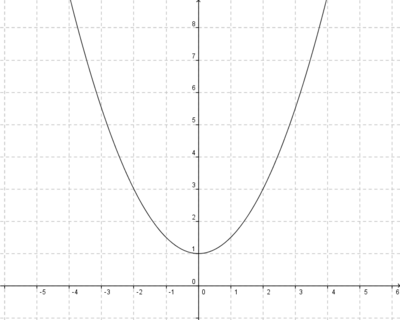
b)
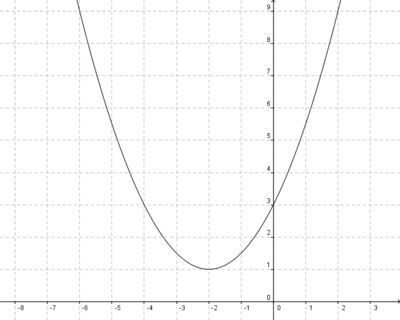
c)
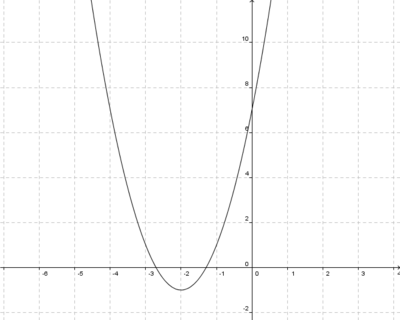
d)
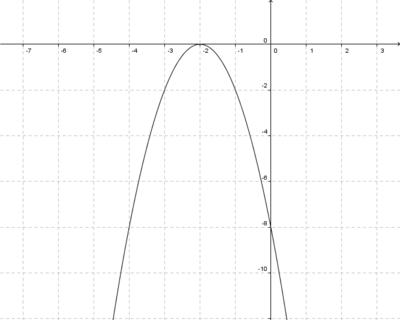
e)
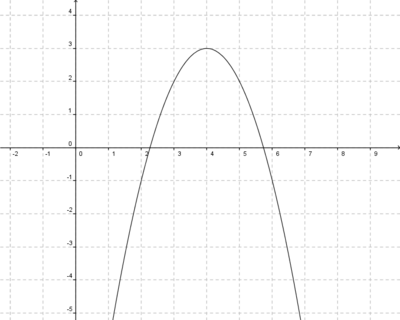
Aufgabe 2:
Gegeben ist die Funktion f(x)=4x6+8x5-12x4-24x3
a) Bestimme die Definitionsmenge
b) Berechne die Nullstellen
c) Bestimme das Verhalten der Funktion an den Rändern des Definitionsbereichs
Aufgabe 3:
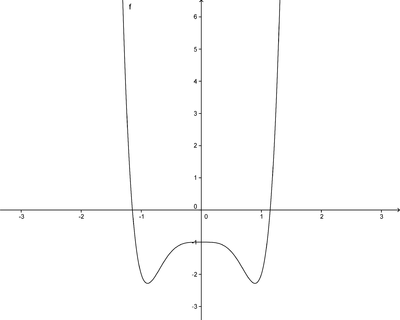
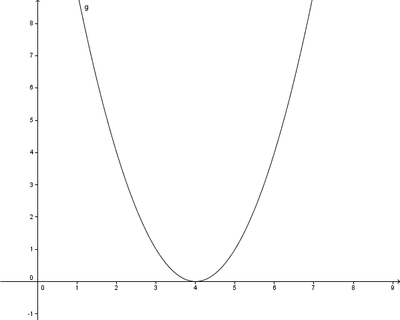
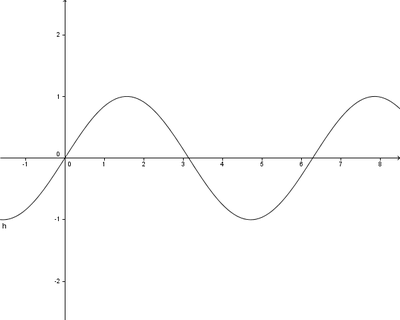
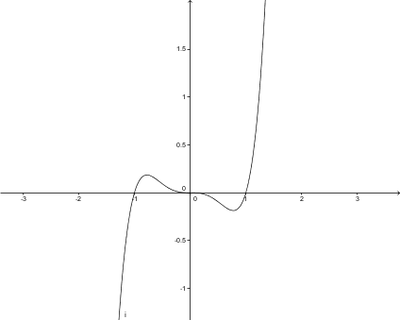
Ordne die folgenden Eigenschaften und Begriffe den unten abgebildeten Graphen zu. Es können bei jeder Funktion mehrere Begriffe richtig sein und einige Begriffe können mehrmals vorkommen.
a. Achsensymmetrie zur y-Achse
b. Nullstelle bei x=4
c. Ganzrationale Funktion
d. Gerade Funktion
e. Trigonometrische Funktion
f. Punktsymmetrie zum Ursprung
g. Ungerade Funktion
 Streckung um 0,5 in y-Richtung
Streckung um 0,5 in y-Richtung 
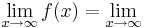 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=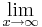 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=
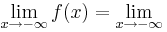 4x6+8x5-12x4-24x3=
4x6+8x5-12x4-24x3=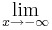 4x3(x3+2x2-3x-6)=
4x3(x3+2x2-3x-6)=