Lösung zur Teilaufgabe b): Unterschied zwischen den Versionen
(→2. Bestimmung einer Stammfunktion von fa durch partielle Integration) |
|||
| Zeile 5: | Zeile 5: | ||
2.)Bei <math>x = a</math> ist der Graph G<sub>f<sub>a</sub></sub> gleich Null ( G<sub>f<sub>a</sub></sub> = 0 )und das Steiguungsverhalten von G<sub>F<sub>a</sub></sub> ändertfür <math>x < a</math> und <math>x > a</math> das Vorzeichen. Deshalb kann man sagen das der Graph G<sub>F<sub>a</sub></sub> an der Stell <math>x = a</math> einen Extrempunkt, in diesem Fall einen Tiefpunkt ( Minimum ) hat, da sich das Monotonieverhalten von streng monoton fallend in streng monoton steigend verändert. | 2.)Bei <math>x = a</math> ist der Graph G<sub>f<sub>a</sub></sub> gleich Null ( G<sub>f<sub>a</sub></sub> = 0 )und das Steiguungsverhalten von G<sub>F<sub>a</sub></sub> ändertfür <math>x < a</math> und <math>x > a</math> das Vorzeichen. Deshalb kann man sagen das der Graph G<sub>F<sub>a</sub></sub> an der Stell <math>x = a</math> einen Extrempunkt, in diesem Fall einen Tiefpunkt ( Minimum ) hat, da sich das Monotonieverhalten von streng monoton fallend in streng monoton steigend verändert. | ||
| + | |||
=== 2. Bestimmung einer Stammfunktion von f<sub>a</sub> durch partielle Integration === | === 2. Bestimmung einer Stammfunktion von f<sub>a</sub> durch partielle Integration === | ||
| Zeile 10: | Zeile 11: | ||
[http://de.wikipedia.org/wiki/Partielle_Integration Hilfe zur partiellen Integration] | [http://de.wikipedia.org/wiki/Partielle_Integration Hilfe zur partiellen Integration] | ||
| − | <math> \ | + | <math> \int_{a}^{b} </math> f<sub>a</sub> ( x ) dx = ( x - a ) e<sup>a + 2 - x</sup> <br /> |
Definiere: | Definiere: | ||
| Zeile 20: | Zeile 21: | ||
v <sup>'</sup> ( x ) = -e<sup>a + 2 - x</sup> | v <sup>'</sup> ( x ) = -e<sup>a + 2 - x</sup> | ||
| − | <math> \ | + | <math> \int_{a}^{b} </math> f<sub>a</sub> ( x ) dx = ( x - a ) e<sup>a + 2 - x</sup> <br /> |
| − | = [( x - a ) -e<sup>a + 2 - x</sup> ]- <math>\ | + | = [( x - a ) -e<sup>a + 2 - x</sup> ]<sup>b</sup><sub>a</sub> - <math> \int_{a}^{b} </math> 1 -e<sup>a + 2 - x</sup> dx |
= ( x - a ) -e<sup>a + 2 - x</sup> - e<sup>a + 2 - x</sup> | = ( x - a ) -e<sup>a + 2 - x</sup> - e<sup>a + 2 - x</sup> | ||
= -e<sup>a + 2 - x</sup> ( x - a + 1 ) | = -e<sup>a + 2 - x</sup> ( x - a + 1 ) | ||
| − | + | ||
| + | --> F<sub>a</sub> ( x ) = -e<sup>a + 2 - x</sup> ( x - a + 1 ) + c | ||
für Interessierte: [[Der Holzweg]] | für Interessierte: [[Der Holzweg]] | ||
| + | |||
| + | |||
| + | === 3. Flächenberechnung, der sich nach rechts ins Unendliche erstreckenden Fläche, zwischen der x- Achse und der Funktion f<sub>2</sub> im I. Quadranten === | ||
| + | |||
| + | ::Hinweis: <math>\lim_{x\to\infty}</math>'''xe<sup>-x</sup> =0''' | ||
| + | |||
| + | Da die Nullstelle der Funktion f<sub>a</sub> bei x = a liegt, folgt daraus, das die Nullstelle der Funktion f<sub>2</sub> bei x = 2 liegt. Das heißt, man muss von zwei bis unendlich integrieren. | ||
| + | |||
| + | <math>\int_{2}^{b}</math> f<sub>2</sub> ( x ) = | ||
Version vom 4. Januar 2010, 00:24 Uhr
1. Eigenschaften einer Stammfunktion von fa
1.) Von 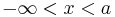 verläuft der Graph Gfa unterhalb der x-Achse und ist somit negative. Daraus kann man schließen, das der Graph GFa in diesem Intervall streng monoton fallend ist.
verläuft der Graph Gfa unterhalb der x-Achse und ist somit negative. Daraus kann man schließen, das der Graph GFa in diesem Intervall streng monoton fallend ist.
Von 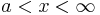 verläuft der Graph Gfa oberhalb der x-Achse und ist somit positive. Daraus kann man schließen, das der Graph GFa in diesem Intervall streng monoton steigend ist.
verläuft der Graph Gfa oberhalb der x-Achse und ist somit positive. Daraus kann man schließen, das der Graph GFa in diesem Intervall streng monoton steigend ist.
2.)Bei  ist der Graph Gfa gleich Null ( Gfa = 0 )und das Steiguungsverhalten von GFa ändertfür
ist der Graph Gfa gleich Null ( Gfa = 0 )und das Steiguungsverhalten von GFa ändertfür 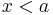 und
und 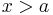 das Vorzeichen. Deshalb kann man sagen das der Graph GFa an der Stell
das Vorzeichen. Deshalb kann man sagen das der Graph GFa an der Stell  einen Extrempunkt, in diesem Fall einen Tiefpunkt ( Minimum ) hat, da sich das Monotonieverhalten von streng monoton fallend in streng monoton steigend verändert.
einen Extrempunkt, in diesem Fall einen Tiefpunkt ( Minimum ) hat, da sich das Monotonieverhalten von streng monoton fallend in streng monoton steigend verändert.
2. Bestimmung einer Stammfunktion von fa durch partielle Integration
Hilfe zur partiellen Integration
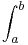 fa ( x ) dx = ( x - a ) ea + 2 - x
fa ( x ) dx = ( x - a ) ea + 2 - x
Definiere:
u ( x ) = x - a
u ' ( x ) = 1
v ( x ) = ea + 2 - x
v ' ( x ) = -ea + 2 - x
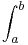 fa ( x ) dx = ( x - a ) ea + 2 - x
fa ( x ) dx = ( x - a ) ea + 2 - x
= [( x - a ) -ea + 2 - x ]ba -1 -ea + 2 - x dx = ( x - a ) -ea + 2 - x - ea + 2 - x = -ea + 2 - x ( x - a + 1 )
--> Fa ( x ) = -ea + 2 - x ( x - a + 1 ) + c
für Interessierte: Der Holzweg
3. Flächenberechnung, der sich nach rechts ins Unendliche erstreckenden Fläche, zwischen der x- Achse und der Funktion f2 im I. Quadranten
- Hinweis:
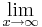 xe-x =0
xe-x =0
- Hinweis:
Da die Nullstelle der Funktion fa bei x = a liegt, folgt daraus, das die Nullstelle der Funktion f2 bei x = 2 liegt. Das heißt, man muss von zwei bis unendlich integrieren.
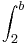 f2 ( x ) =
f2 ( x ) =

