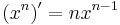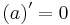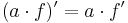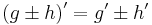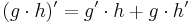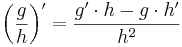Q11 Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
(+interaktiv) |
(lösungen kapitel3 verlinkt) |
||
| Zeile 124: | Zeile 124: | ||
</td></tr></table></center> | </td></tr></table></center> | ||
| + | |||
| + | Lösungen [http://www.klett.de/sixcms/media.php/71/732763_LS_BY_11_K1.pdf Kapitel I] - [http://www.klett.de/sixcms/media.php/71/732763_LS_BY_11_K2_LE_1_8.pdf Kapitel II] - [http://www.klett.de/sixcms/media.php/71/732763_LS_BY_11_K3_LE_1_5.pdf Kapitel III] | ||
</div> | </div> | ||
Version vom 6. Dezember 2009, 18:49 Uhr
1. Gebrochenrationale FunktionenLösungen Buch: Lösungen AH: |
2. Differenzenquotient - mittlere Änderungsrate -Steigung Sekante |
3. Differentialquotient - lokale Änderungsrate - Steigung Tangente
|
4. Ableitungsfunktion
|
5. Ableitungsregeln
|
6. Monotonie, Extrema |
|
7. Kurvendiskussion |
Lösungen Kapitel I - Kapitel II - Kapitel III