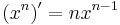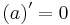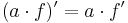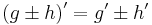Q11 Mathematik: Unterschied zwischen den Versionen
Aus RMG-Wiki
| Zeile 77: | Zeile 77: | ||
#[[Q11 Mathematik/LS11 Seite 52_12_14|Lösung Seite 51/12 und 14]] | #[[Q11 Mathematik/LS11 Seite 52_12_14|Lösung Seite 51/12 und 14]] | ||
#<font color="green">Interaktiv:</font> [[Q11 Mathematik/Seite 51_8|Seite 51/8]] | #<font color="green">Interaktiv:</font> [[Q11 Mathematik/Seite 51_8|Seite 51/8]] | ||
| + | #Lösungen Buch: [[Q11 Mathematik/Seite48_2 Seite 51_4|48/2 und 51/4]] | ||
|width="5%"|<!--Diese Spalte bleibt leer und legt den Abstand zwischen Text und Bild fest--> | |width="5%"|<!--Diese Spalte bleibt leer und legt den Abstand zwischen Text und Bild fest--> | ||
|valign="top" | | |valign="top" | | ||
Version vom 13. November 2009, 00:36 Uhr
1. Gebrochenrationale FunktionenLösungen Buch: Lösungen AH: |
2. Differenzenquotient - mittlere Änderungsrate -Steigung Sekante |
3. Differentialquotient - lokale Änderungsrate - Steigung Tangente
|
4. Ableitungsfunktion
|
5. Ableitungsregeln
|