Schluss: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Lösung eingefügt) |
K (Lösung eingefügt) |
||
| Zeile 87: | Zeile 87: | ||
==Aufgabe 3== | ==Aufgabe 3== | ||
{{Lösung versteckt| | {{Lösung versteckt| | ||
| + | *Die Bilddiagonale ist die Hypotenuse eines rechtwinkligen Dreiecks (vgl. Grafik zu Aufgabe 20 in deinem Mathematik Buch auf S.48) | ||
| + | *Die Katheten verhalten sich dabei wie 16 Teile zu 9 Teilen | ||
| + | *Wähle ein Teil als <math>{x\,}</math> | ||
| + | *Damit hat die Breite <math>{16x\,}</math> und die Höhe <math>{9x\,}</math> | ||
| + | *Damit kann man den Satz des Pythagoras für das rechtwinklige Dreieck ansetzen:<br /> | ||
| + | *<math>{(80cm)^2=(16x)^2+(9x)^2\,}</math> | ||
| + | *<math>{6400cm^2=256x^2+81x^2\,}</math> | ||
| + | *<math>{6400cm^2=337x^2\,}</math> | ||
| + | *<math>x^2=\frac{6400}{337}cm^2</math> | ||
| + | *<math>x=\sqrt{\frac{6400}{337}}cm \approx 4,36cm</math><br /><br /> | ||
| + | Die Breite beträgt <math>{16x\,}</math> | ||
| + | *<math>{b=16 \cdot 4,36cm=69,76cm\,}</math> | ||
| + | *<math>69,76cm < 75cm \Rightarrow</math> Der Fernseher passt in die Nische | ||
}} | }} | ||
==Aufgabe 4== | ==Aufgabe 4== | ||
Version vom 25. Januar 2009, 15:17 Uhr
Arbeitsauftrag:
- Hole dir das Arbeitsblatt Die Satzgruppe des Pythagoras
- Fülle das Arbeitsblatt anhand der im Lernpfad gelernten Sätze aus
- HINWEIS: Solltest du dir bei einem der Sätze nicht mehr sicher sein, lies noch einmal im Heft oder im Lernpfad nach
- Vergleiche deine Lösungen mit den Einträgen aus dem Heft oder mit den entsprechenden Seiten des Lernpfades
Arbeitsauftrag:
- Hole dir das Übungsblatt zur Satzgruppe des Pythagoras
- Löse die Aufgaben und vergleiche sie mit den unten stehenden Lösungen
Aufgabe 1
rechtwinklig ist, ergibt der Satz des Pythagoras eine wahre Aussage
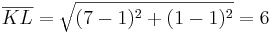
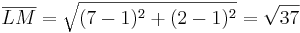
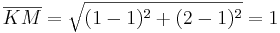
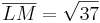ist die längste Seite des Dreiecks und wäre auch die Hypotenuse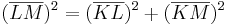
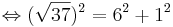
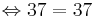
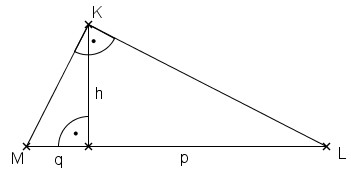
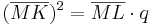
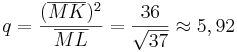
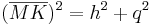
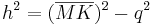
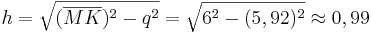
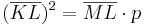
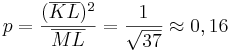
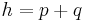
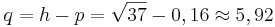
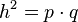
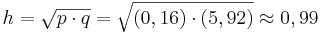
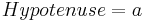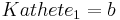Aufgabe 2
, 
und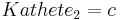 
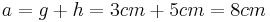
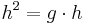
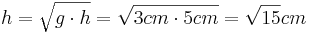
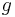anliegend an 
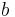und 
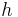anliegend an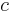 
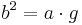
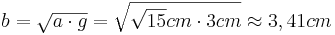
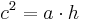
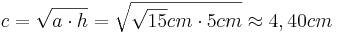
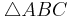berechnet werden
Aufgabe 3
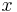
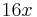und die Höhe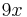 
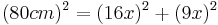
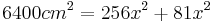
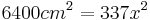
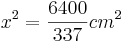
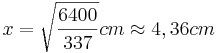
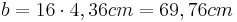
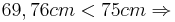Der Fernseher passt in die Nische
Aufgabe 4
Aufgabe 5
Sehr schön! Du hast den Lernpfad zur Satzgruppe des Pythagoras jetzt beendet 
