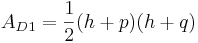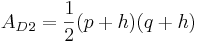Höhensatz: Unterschied zwischen den Versionen

Aus RMG-Wiki
Wechseln zu: Navigation, Suche
(Grafik und Seitenbeschreibung eingefügt)
 
K
 
(9 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt)
Zeile 12: Zeile 12:
 
''Bevor du dich jedoch näher mit diesem Satz beschäftigst, musst du erst noch einige neue Bezeichnungen für Seiten in rechtwinkligen Dreiecken lernen:''<br /><br />
 
''Bevor du dich jedoch näher mit diesem Satz beschäftigst, musst du erst noch einige neue Bezeichnungen für Seiten in rechtwinkligen Dreiecken lernen:''<br /><br />
  
−
*Die Höhe in einem rechtwinkligen Dreieck wird meistens mit h bezeichnet
+
*Die Höhe in einem rechtwinkligen Dreieck steht '''immer''' senkrecht auf die Hypotenuse<br /><br />
−
*Die Höhe steht '''immer''' senkrecht auf die Hypotenuse<br /><br />
+
  
−
*Die Höhe teilt die Hypotenuse in zwei Teile, die '''Hypotenusenabschnitte''' (in der Zeichnung p und q)<br /><br />
+
*Die Höhe teilt die Hypotenuse in zwei Teile, die '''Hypotenusenabschnitte'''<br />(in der Zeichnung <span style="color: blue">'''p'''</span> und <span style="color: red">'''q'''</span>)<br /><br />
 
*Die Hypotenuseabschnitte liegen jeweils an '''einer''' der beiden Katheten an
 
*Die Hypotenuseabschnitte liegen jeweils an '''einer''' der beiden Katheten an
−
*p liegt an a an
+
*In '''diesem''' Fall kann man sagen:
−
*q liegt an b an
+
*p liegt an der Kathete a an
 +
*q liegt an der Kathete b an
 +
|}<br /><br />
 +
<div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white;  width:90%; align:center; ">
 +
<span style="color: green">'''Arbeitsauftrag:'''</span>
 +
*Zeichne das oben stehende rechtwinklige Dreieck mit den Seitenbezeichnungen unter der Überschrift ''Der Höhensatz'' in dein Heft
 +
 
 +
*Notiere dir die Bemerkungen rechts vom rechtwinkligen Dreieck
 +
 
 +
*Wenn du damit fertig bist betrachte die folgenden Grafiken</div><br /><br />
 +
 
 +
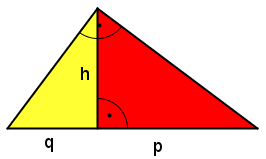
*Ausgangspunkt für die folgende Überlegung ist ein rechtwinkliges Dreieck mit der ''Höhe h'' und den ''Hypotenusenabschnitten p und q''<br />
 +
[[Bild:Beweis zu Höhensatz 1.png]]<br />
 +
 
 +
----
 +
 
 +
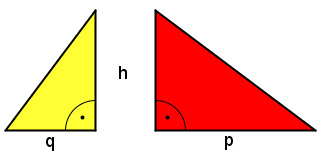
*Aus diesem rechtwinkligen Dreieck kann man zwei kleinere rechtwinklige Dreiecke machen
 +
*Eines hat als Länge der Katheten p und h, das andere hat Katheten der Längen q und h<br />
 +
[[Bild:Beweis zu Höhensatz 2.png]]<br /><br />
 +
 
 +
----
 +
 
 +
 
 +
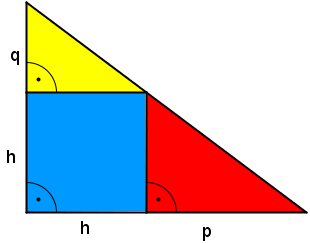
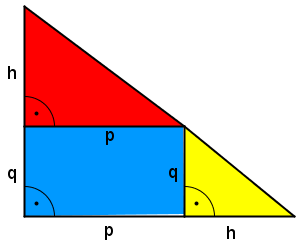
*Diese beiden rechtwinkligen Dreiecke kann man nun verschieden aneinander anlegen und so ein neues rechtwinkliges Dreieck erzeugen
 +
*Die zwei Möglichkeiten neue rechtwinklige Dreiecke zu erzeugen seht ihr in den beiden folgenden Grafiken
 +
{|width="95%"
 +
| width="10%" style="vertical-align:top" |
 +
| width="37,5%" style="vertical-align:top" |
 +
[[Bild:Beweis zu Höhensatz 3a.png]]
 +
 
 +
| width="5%" style="vertical-align:top" |
 +
| width="37,5%%" style="vertical-align:top" |
 +
[[Bild:Beweis zu Höhensatz 3b.png]]
 +
 
 +
| width="10%" style="vertical-align:top" |
 
|}
 
|}
 +
 +
<div style="margin:0px; margin-right:90px; border:thick double green; padding: 1em 1em 1em 1em; background-color:white;  width:90%; align:center; ">
 +
<span style="color: green">'''Arbeitsauftrag:'''</span>
 +
*Hole dir das Arbeitsblatt '''Beweis zum Höhensatz'''
 +
 +
*Berechne auf dem Arbeitsblatt den Flächeninhalt der beiden unten stehenden Dreiecke!
 +
 +
*''Was fällt dir auf?''
 +
 +
*''Was kann man daraus für den Flächeninhalt der blauen Teile folgern?''</div>
 +
 +
 +
{{Lösung versteckt|
 +
Der Flächeninhalt eines Dreiecks berechnet sich so:
 +
<math>A_{Dreieck}=\frac{1}{2} \cdot G \cdot h</math>
 +
 +
'''Fläche für Dreieck 1:'''<br /><br />
 +
*<math>{A_D}_1=\frac{1}{2}(h+p)(h+q)</math><br /><br />
 +
 +
'''Fläche für Dreieck 2:'''<br /><br />
 +
*<math>{A_D}_2=\frac{1}{2}(p+h)(q+h)</math>
 +
}}
 +
 +
{{Lösung versteckt|
 +
'''Folgerung:'''
 +
*Die Dreiecke sind flächengleich
 +
*In beiden Dreiecken tauchen das rote und das gelbe Dreieck auf
 +
*Der blaue Flächeninhalt in beiden Dreiecken muss also die gleiche Fläche haben, da:
 +
*<math>{A_D}_1={A_D}_2</math>
 +
*<math>{A_{gelb}\,}</math> '''und''' <math>{A_{rot}\,}</math> in beiden Dreiecken gleich<br />
 +
*Daraus folgt:<math>{A_D}_1-A_{rot}-A_{gelb}={A_D}_2-A_{rot}-A_{gelb}=A_{blau}</math><br /><br />
 +
*Das heißt der Flächeninhalt der beiden blauen Teile muss gleich sein
 +
 +
Da <math>{A_{blau}}_1={A_{blau}}_2</math>kann man sagen:<br /><br />
 +
 +
<math>{h^2=pq\,}</math><br /><br />
 +
 +
Denn <math>{A_{blau}}_1=h \cdot h</math> '''und''' <math>{A_{blau}}_2=p \cdot q</math>
 +
 +
 +
*In ''jedem beliebigen rechtwinkligen Dreieck'' gilt also:
 +
*Das Quadrat über der Höhe ist flächengleich zum Rechteck aus den beiden Hypotenusenabschnitten
 +
}}
 +
 +
Du hast den Höhensatz bewiesen. [[Lernpfad zur Satzgruppe des Pythagoras/Hefteintrag zum Höhensatz|Hier]] geht es nun zum Hefteintrag.

Aktuelle Version vom 24. Januar 2009, 19:00 Uhr

Der Höhensatz

Ein weiterer Satz aus der Satzgruppe des Pythagoras ist der Höhensatz.

Benennung rechtwinkliges Dreieck für Höhensatz.png

Bevor du dich jedoch näher mit diesem Satz beschäftigst, musst du erst noch einige neue Bezeichnungen für Seiten in rechtwinkligen Dreiecken lernen:

  • Die Höhe in einem rechtwinkligen Dreieck steht immer senkrecht auf die Hypotenuse

  • Die Höhe teilt die Hypotenuse in zwei Teile, die Hypotenusenabschnitte
    (in der Zeichnung p und q)

  • Die Hypotenuseabschnitte liegen jeweils an einer der beiden Katheten an
  • In diesem Fall kann man sagen:
  • p liegt an der Kathete a an
  • q liegt an der Kathete b an


Arbeitsauftrag:

  • Zeichne das oben stehende rechtwinklige Dreieck mit den Seitenbezeichnungen unter der Überschrift Der Höhensatz in dein Heft
  • Notiere dir die Bemerkungen rechts vom rechtwinkligen Dreieck
  • Wenn du damit fertig bist betrachte die folgenden Grafiken


  • Ausgangspunkt für die folgende Überlegung ist ein rechtwinkliges Dreieck mit der Höhe h und den Hypotenusenabschnitten p und q

Beweis zu Höhensatz 1.png

  • Aus diesem rechtwinkligen Dreieck kann man zwei kleinere rechtwinklige Dreiecke machen
  • Eines hat als Länge der Katheten p und h, das andere hat Katheten der Längen q und h

Beweis zu Höhensatz 2.png


  • Diese beiden rechtwinkligen Dreiecke kann man nun verschieden aneinander anlegen und so ein neues rechtwinkliges Dreieck erzeugen
  • Die zwei Möglichkeiten neue rechtwinklige Dreiecke zu erzeugen seht ihr in den beiden folgenden Grafiken

Beweis zu Höhensatz 3a.png

Beweis zu Höhensatz 3b.png

Arbeitsauftrag:

  • Hole dir das Arbeitsblatt Beweis zum Höhensatz
  • Berechne auf dem Arbeitsblatt den Flächeninhalt der beiden unten stehenden Dreiecke!
  • Was fällt dir auf?
  • Was kann man daraus für den Flächeninhalt der blauen Teile folgern?


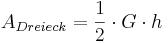
Der Flächeninhalt eines Dreiecks berechnet sich so: A_{Dreieck}=\frac{1}{2} \cdot G \cdot h

Fläche für Dreieck 1:

  • {A_D}_1=\frac{1}{2}(h+p)(h+q)

Fläche für Dreieck 2:

  • {A_D}_2=\frac{1}{2}(p+h)(q+h)

Folgerung:

  • Die Dreiecke sind flächengleich
  • In beiden Dreiecken tauchen das rote und das gelbe Dreieck auf
  • Der blaue Flächeninhalt in beiden Dreiecken muss also die gleiche Fläche haben, da:
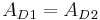
  • {A_D}_1={A_D}_2
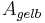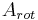  • {A_{gelb}\,} und {A_{rot}\,} in beiden Dreiecken gleich
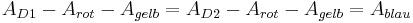
  • Daraus folgt:{A_D}_1-A_{rot}-A_{gelb}={A_D}_2-A_{rot}-A_{gelb}=A_{blau}

  • Das heißt der Flächeninhalt der beiden blauen Teile muss gleich sein

Da 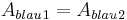{A_{blau}}_1={A_{blau}}_2kann man sagen:

{h^2=pq\,}

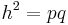
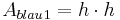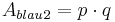
Denn {A_{blau}}_1=h \cdot h und {A_{blau}}_2=p \cdot q


  • In jedem beliebigen rechtwinkligen Dreieck gilt also:
  • Das Quadrat über der Höhe ist flächengleich zum Rechteck aus den beiden Hypotenusenabschnitten

Du hast den Höhensatz bewiesen. Hier geht es nun zum Hefteintrag.

Von „http://rmg.zum.de/index.php?title=Lernpfad_zur_Satzgruppe_des_Pythagoras/Höhensatz&oldid=12326“