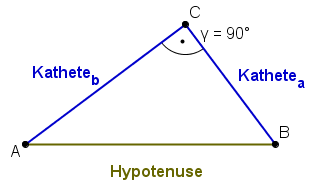
Bezeichnungen im rechtwinkligen Dreieck: Unterschied zwischen den Versionen
Aus RMG-Wiki
(Höhe von Rahmen verändert) |
K |
||
| (4 dazwischenliegende Versionen von einem Benutzer werden nicht angezeigt) | |||
| Zeile 1: | Zeile 1: | ||
{| width="99%" | {| width="99%" | ||
| − | |[[Bild: | + | |[[Bild:Benennungen_in_rechtwinkligen_Dreiecken.png]] |
| width="5%" style="vertical-align:top" | | | width="5%" style="vertical-align:top" | | ||
| Zeile 53: | Zeile 53: | ||
| width="1%" style="vertical-align:top" | | | width="1%" style="vertical-align:top" | | ||
| width="89%" style="vertical-align:top" | | | width="89%" style="vertical-align:top" | | ||
| − | Zeichne ein beliebiges rechtwinkliges Dreieck in dein Heft, trage die Bezeichnungen an die Seiten an und notiere dir die Eigenschaften und die Lage der Seiten! Dein Hefteintrag sollte so aussehen: [[ | + | Zeichne ein beliebiges rechtwinkliges Dreieck in dein Heft, trage die Bezeichnungen an die Seiten an und notiere dir die Eigenschaften und die Lage der Seiten! Dein Hefteintrag sollte so aussehen: [[Lernpfad zur Satzgruppe des Pythagoras/Hefteintrag zum rechtwinkligen Dreieck|>>Hefteintrag]] |
|}</div> | |}</div> | ||
Aktuelle Version vom 24. Januar 2009, 18:55 Uhr
|
Besonderheiten des rechtwinkligen Dreiecks
|
Die Hypotenuse
Betrachte die folgenden rechtwinkligen Dreiecke!
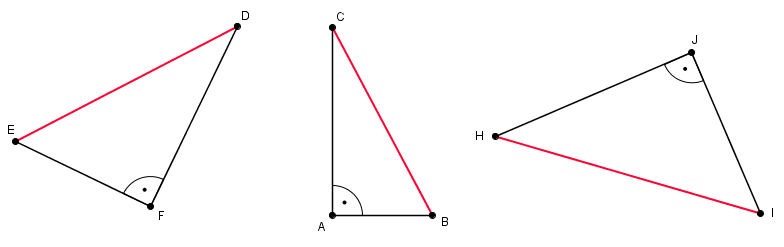
Was fällt dir auf, wenn du die Länge der Hypotenuse mit der der beiden Katheten vergleichst?
Sollte dir nichts auffallen, hier als kleine Hilfe die genauen Längen der einzelnen Seiten:
| |
|
| |
| Kathete1 | 3 | 3,75 | 4,28 |
| Kathete2 | 4 | 2 | 3,5 |
| Hypotenuse | 5 | 4,25 | 5,52 |
Antwort: Die Hypotenuse ist die längste Seite im Dreieck
Hinweis: Das ist nicht nur in diesen drei rechtwinkligen Dreiecken so, sondern es gilt für jedes beliebige rechtwinklige Dreieck!
|
Arbeitsauftrag: |
Zeichne ein beliebiges rechtwinkliges Dreieck in dein Heft, trage die Bezeichnungen an die Seiten an und notiere dir die Eigenschaften und die Lage der Seiten! Dein Hefteintrag sollte so aussehen: >>Hefteintrag |
