Umwandlung Rechteck in Quadrat (K) - Seite 8
Aus RMG-Wiki
< Lernpfad zur Satzgruppe des Pythagoras(Weitergeleitet von Umwandlung 8)
Zusammenfassung
Idee:
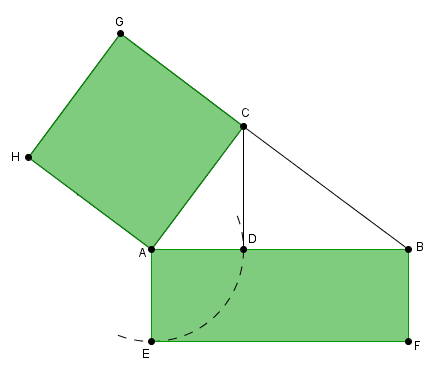
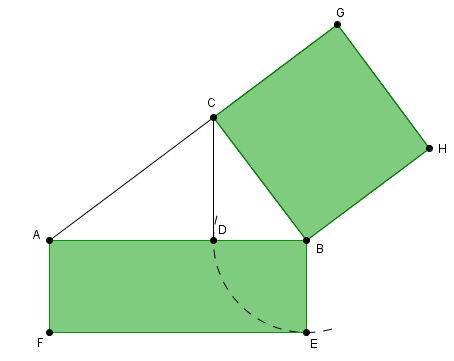
- Ein rechtwinkliges Dreieck so konstruieren, dass das gegebene Rechteck, das Rechteck aus der Hypotenuse und einem Hypotenusenabschnitt ist
- Die längere der beiden Rechtecksseiten ist die Hypotenuse
Vorgehen:
- Die Kürzere der beiden Rechtecksseiten mit Hilfe eines Kreises an die Längere antragen
- Der Schnittpunkt des Kreises mit längeren Rechtecksseite teilt diese in zwei Teile
- Einen Thaleskreis über die längere Rechtecksseite zeichnen
- Senkrechte zur längeren Rechtecksseite durch den Schnittpunkt des Kreises mit der längeren Rechtecksseite zeichnen
- Schnittpunkt der Senkrechten mit dem Thaleskreis ist dritter Punkt des gesuchten rechtwinkligen Dreiecks
- ACHTUNG: Das Quadrat wird über der Kathete gezeichnet, die am angetragenen Hypotenusenabschnitt anliegt
- Das Quadrat über dieser Kathete ist flächengleich zum Rechteck aus Hypotenuse und dem an der Kathete anliegenden Hypotenusenabschnitt, oder
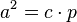 bzw.
bzw. 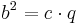
- WICHTIG: Je nachdem an welcher Ecke du die kürzere Seite des Rechtecks anträgst, verändert sich auch die Kathete, welche du für das Quadrat wählen musst (sieh dir hierzu die unten stehenden Grafiken an)
Arbeitsauftrag:
- Gehe die einzelnen Schritte anhand der Zusammenfassung oben noch ein mal durch
- Übertrage die Zusammenfassung in dein Heft
Wenn du den Hefteintrag fertig hast geht es hier mit einer Übung weiter