Lösung zum Übungsblatt zum Kathetensatz (Aufgabe 6)
Aus RMG-Wiki
< Lernpfad zur Satzgruppe des Pythagoras(Weitergeleitet von Lernpfad zur Satzgruppe des Pythagoras/Übung Umwandlung)
Arbeitsauftrag:
- Löse die Aufgabe 6 vom Übungsblatt zum Kathetensatz im Heft und vergleiche deine Lösung mit der auf der Seite
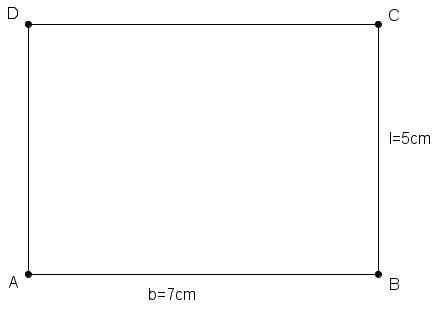
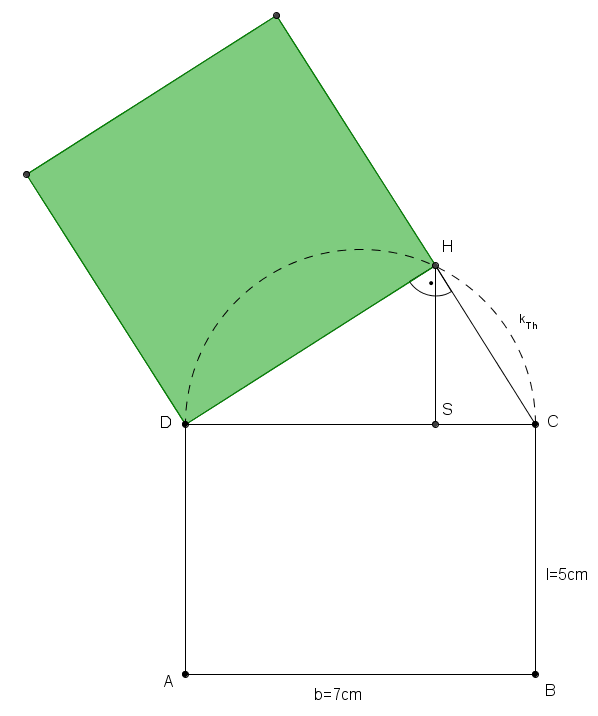
Aufgabe 6
Hinweis:
- Wie bei der Umwandlung eines Rechtecks in ein flächengleiches Quadrat mit Hilfe des Höhensatzes, kannst du auch hier dein konstruiertes Quadrat rechnerisch überprüfen
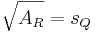 , wobei
, wobei 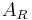 der Flächeninhalt des gegebenen Rechtecks und
der Flächeninhalt des gegebenen Rechtecks und 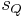 die Länge des von dir konstruierten Quadrats ist
die Länge des von dir konstruierten Quadrats ist
Wenn du fertig bist geht es hier weiter
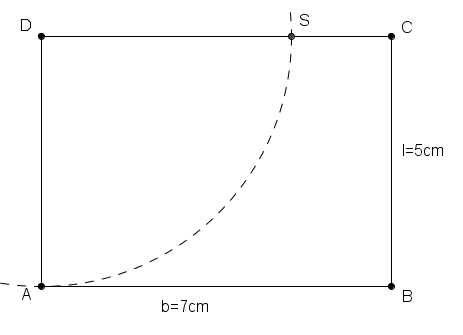
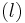 an die längere
an die längere 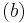 an und erhält dadurch einen Schnittpunkt
an und erhält dadurch einen Schnittpunkt 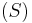
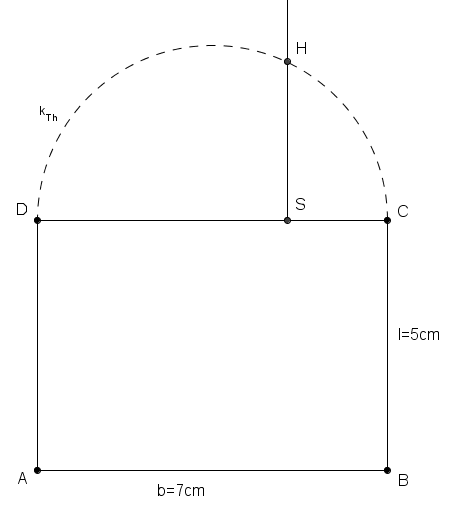
![{[DC]\,}](/images/math/b/b/a/bba0b66040f07b2a2dbcc8eb039a4c5e.png)
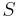
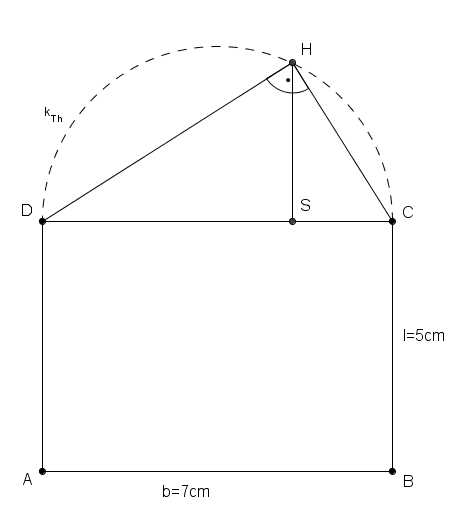
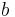 angetragenen Rechtecksseite liegt
angetragenen Rechtecksseite liegt