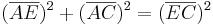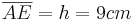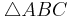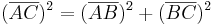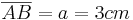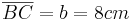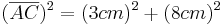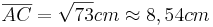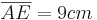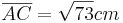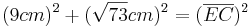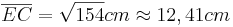Diagonalenberechnung - Seite 2
Aus RMG-Wiki
< Lernpfad zur Satzgruppe des Pythagoras(Weitergeleitet von Lernpfad zur Satzgruppe des Pythagoras/Diagonalenberechnung 2)
Arbeitsauftrag:
- Vergleiche deine Idee mit der Lösung
- Solltest du keine Idee haben, gehe die Schritte langsam druch, vielleicht fällt dir die Lösung doch noch auf
- Übertrage die Rechnung in dein Heft
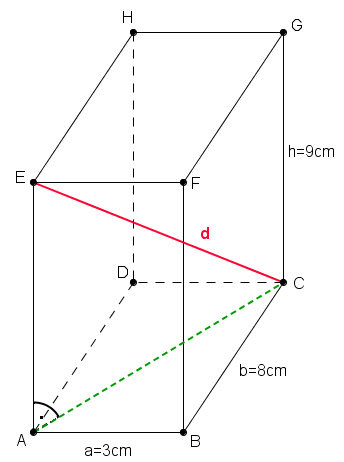
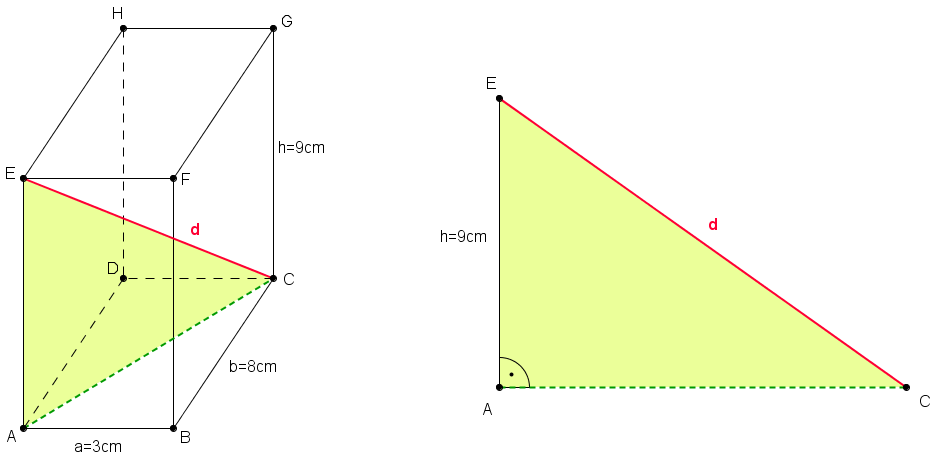
- Die Länge des Strohhalms ist eine Diagonale des Quaders
- Die Diagonale liegt im rechtwinkligen Dreieck
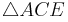
- Die Länge der Strecke
![{[AC]\,}](/images/math/7/5/5/7551fad9ac50fcbce678dda8cf22f59f.png) kann man mit Hilfe des Satzes des Pythagoras berechnen
kann man mit Hilfe des Satzes des Pythagoras berechnen
- Die Länge beträgt:
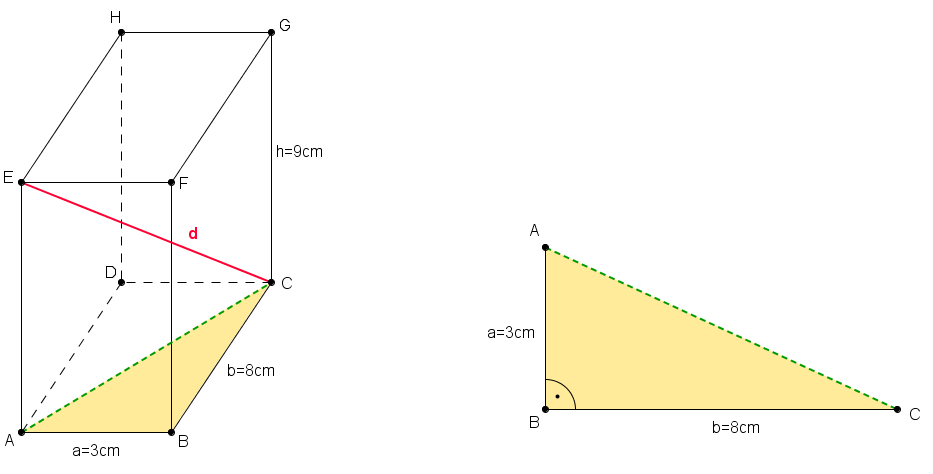
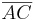 ist noch unbekannt und muss berechnet werden
ist noch unbekannt und muss berechnet werden
Wenn du fertig bist geht es hier weiter