Arbeitsauftrag:
- Hole dir das Übungsblatt zum Satz des Pythagoras
- Berechne die einzelnen Aufgaben
- Vergleiche deine Lösungen mit denen auf der Seite
Aufgabe 1
|
|
|
[Lösung anzeigen][Lösung ausblenden]
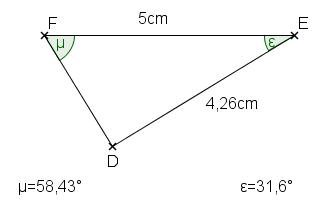
- Das Dreieck ist nicht rechtwinklig, da der fehlende Winkel 89,97° beträgt
- Man kann den Satz des Pythagoras also nicht anwenden da es sich um kein rechtwinkliges Dreieck handelt
|
|
|
|
[Lösung anzeigen][Lösung ausblenden]
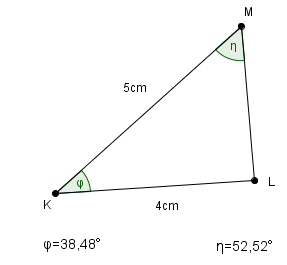
- Es handelt sich um kein rechtwinkliges Dreieck, da der dritte Winkel im Dreieck 89° beträgt
- Der Satz des Pythagoras kann also nicht angewendet werden, da nur eine Verwendung in rechtwinkligen Dreiecken möglich ist
|
|
|
|
[Lösung anzeigen][Lösung ausblenden]
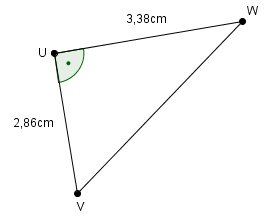
- Es handelt sich um ein rechtwinkliges Dreieck
- Die Hypotenuse (u) wird gesucht, Kathete1 (w) ist 2,86cm und Kathete2 (v) ist 3,38cm lang
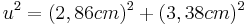
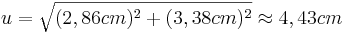
- Die Hypotenuse (u) ist etwa 4,43cm lang
|
Aufgabe 2
[Lösung anzeigen][Lösung ausblenden]
Es gibt ein rechtwinkliges Dreieck
Die Katheten sind 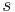 und
und 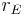 , die Hypotenuse hat die Länge
, die Hypotenuse hat die Länge 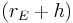
Daraus ergibt sich der Ansatz:
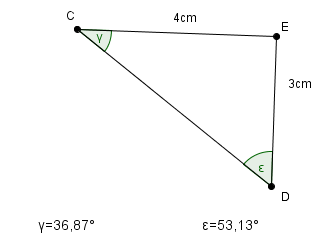
Aufgabe 3
[Lösung anzeigen][Lösung ausblenden]
Wenn du fertig mit den Aufgaben bist, geht es hier weiter.
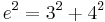
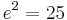
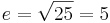



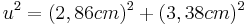
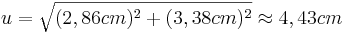
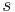 und
und 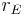 , die Hypotenuse hat die Länge
, die Hypotenuse hat die Länge 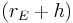
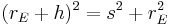
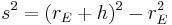
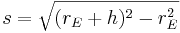
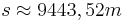
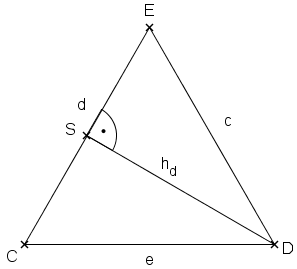
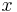 sei die Länge der Seiten
sei die Länge der Seiten
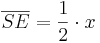
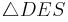 den Satz des Pythagoras ansetzen:
den Satz des Pythagoras ansetzen:
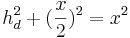
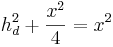
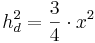
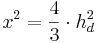
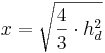
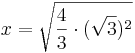
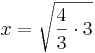
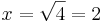
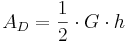
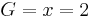 ,
,