Durchgeflossenes Wasservolumen nach t = 24: Unterschied zwischen den Versionen
Aus RMG-Wiki
(→Wasserstand nach 24 Monaten) |
(→Durchflossenes Wasservolumen nach 24 Monaten) |
||
| Zeile 18: | Zeile 18: | ||
====Durchflossenes Wasservolumen nach 24 Monaten==== | ====Durchflossenes Wasservolumen nach 24 Monaten==== | ||
| − | + | [[Bild:Beispiel für Theorie.jpg|right]] | |
<math>\int_{0}^{24} F (x)\,dx = \left[ \frac{1}{16}t^4 - t^3 + \frac{9}{2}t^2 \right]_{0}^{24}</math> | <math>\int_{0}^{24} F (x)\,dx = \left[ \frac{1}{16}t^4 - t^3 + \frac{9}{2}t^2 \right]_{0}^{24}</math> | ||
Version vom 16. Januar 2010, 19:50 Uhr
Inhaltsverzeichnis |
Beispielaufgabe zur Verdeutlichung
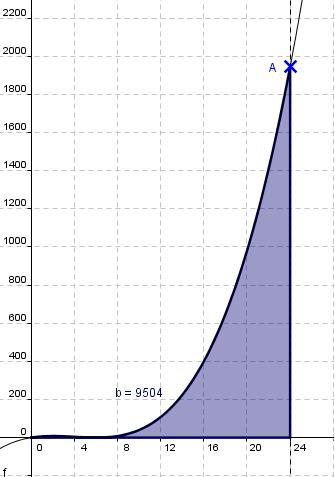
In diesem Beispiel soll für t = 24 und a = 3 zum einen der Wasserstand zum Zeitpunkt t errechnet werden und anschließend das Gesamtvolumen an Wasser, welches seit Beginn (t = 0) durch den Fluss geflossen ist.
gegeben:
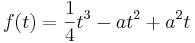 ; t = 24; a = 3
; t = 24; a = 3
Wasserstand nach 24 Monaten
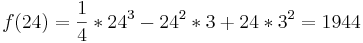
Das Ergebnis wäre also 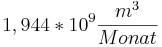 .
.
Dieser Wasserstandswert ist sicherlich eine ziemlich grobe Abweichung vom Realwert.
Durchflossenes Wasservolumen nach 24 Monaten
![\int_{0}^{24} F (x)\,dx = \left[ \frac{1}{16}t^4 - t^3 + \frac{9}{2}t^2 \right]_{0}^{24}](/images/math/c/3/5/c350c0785737379aefea9211dd6cfad4.png)
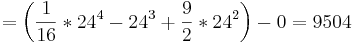
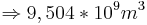 wären also in den ersten 24 Monaten durch den Fluss geflossen.
wären also in den ersten 24 Monaten durch den Fluss geflossen.
- Wäre t noch viel viel größer, wäre das errechnete Ergebnis noch viel unrealistischer, da es exponential größer werden würde.
Ergebnis
Aus diesem Grund handelt es sich bei der Funktion eher um eine Sinusähnliche Funktion, da man bei einer Potenzfunktion wie hier, bei wachsendem t, immer unrealistischere Werte bekommt.