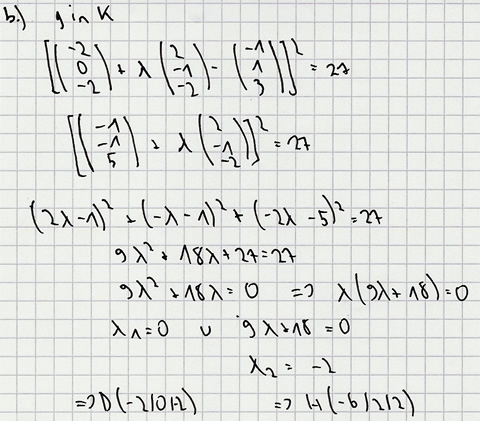2005 V: Unterschied zwischen den Versionen
(Die Seite wurde neu angelegt: __NOTOC__ <div style="padding:1px;background: #EEEEE6;border:0px groove;"> <center><table border="0" width="800px" cellpadding=5 cellspacing=15> <tr><td width="800px...) |
(Bewertungseinheiten und Bildnamen korrigiert) |
||
| Zeile 44: | Zeile 44: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2005_V_1a_Lös.jpg|750px]] |
}} | }} | ||
| Zeile 51: | Zeile 51: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2005_V_1b_Lös.jpg|750px]] |
}} | }} | ||
| Zeile 70: | Zeile 70: | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2005_V_1c_Lös.jpg|750px]] |
}} | }} | ||
| Zeile 76: | Zeile 76: | ||
d) Zeigen Sie, dass die Scharebene Z2 eine winkelhalbierende Ebene der beiden zueinander senkrechten Scharebenen Z<sub>1</sub> und Z<sub>4 </sub>ist. ''5 BE'' | d) Zeigen Sie, dass die Scharebene Z2 eine winkelhalbierende Ebene der beiden zueinander senkrechten Scharebenen Z<sub>1</sub> und Z<sub>4 </sub>ist. ''5 BE'' | ||
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2005_V_1d_Lös.jpg|750px]] |
}} | }} | ||
| Zeile 86: | Zeile 86: | ||
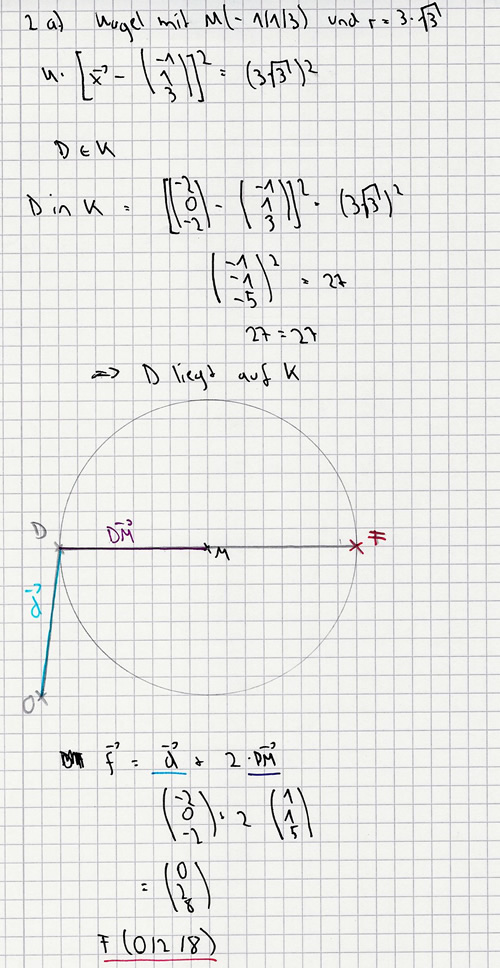
| − | a)Zeigen Sie, dass der Punkt D auf dieser Kugel liegt, und berechnen Sie die Koordinaten des Kugelpunkts F, für den [FD] ein Durchmesser der Kugel ist. | + | a)Zeigen Sie, dass der Punkt D auf dieser Kugel liegt, und berechnen Sie die Koordinaten des Kugelpunkts F, für den [FD] ein Durchmesser der Kugel ist. [Ergebnis: F(0 | 2 | 8)] ''4 BE'' |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2005_V_2a_Lös.jpg|750px]] |
}} | }} | ||
| − | b) Bestimmen Sie die Koordinaten der Kugelpunkte, die auf der Geradeng liegen. | + | b) Bestimmen Sie die Koordinaten der Kugelpunkte, die auf der Geradeng liegen. [Ergebnis: D und H(-6 | 2 | 2) ] ''6 BE'' |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2005_V_2b_Lös.jpg|750px]] |
}} | }} | ||
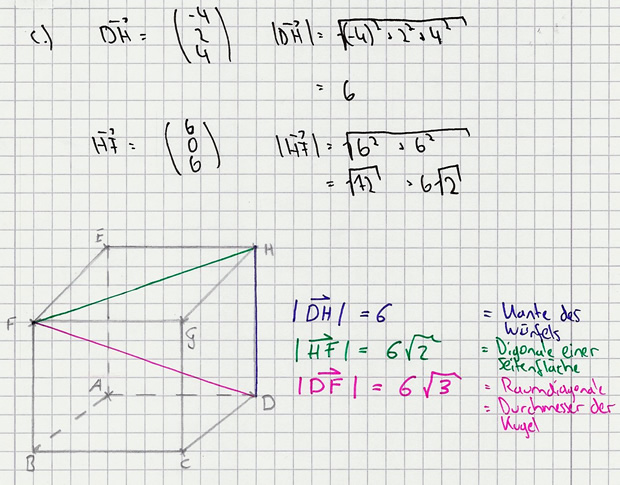
| − | c) Berechnen Sie die Längen DH und HF und begründen Sie, dass man die drei Punkte D, F und H zu einem Würfel ABCDEFGH wie in der Abbildung ergänzen kann. | + | c) Berechnen Sie die Längen DH und HF und begründen Sie, dass man die drei Punkte D, F und H zu einem Würfel ABCDEFGH wie in der Abbildung ergänzen kann. ''6 BE'' |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2005_V_2c_Lös.jpg|750px]] |
}} | }} | ||
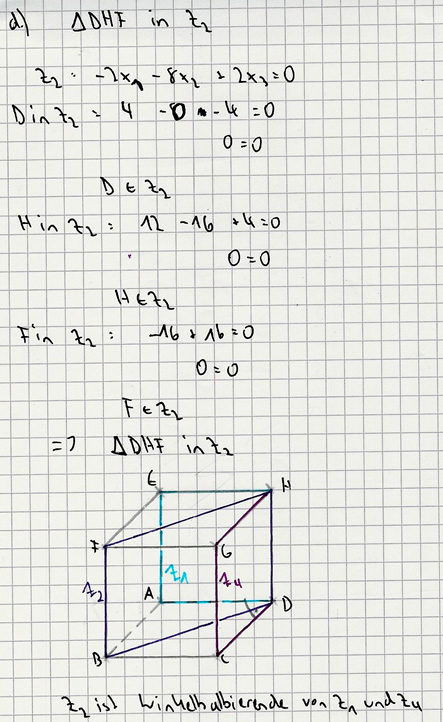
d) Zeigen Sie, dass das Dreieck DHF in der Ebene Z<sub>2</sub> liegt. Begründen Sie ohne Rechnung nur mit Hilfe der bisherigen Ergebnisse, warum | d) Zeigen Sie, dass das Dreieck DHF in der Ebene Z<sub>2</sub> liegt. Begründen Sie ohne Rechnung nur mit Hilfe der bisherigen Ergebnisse, warum | ||
| − | die Ebenen Z<sub>1</sub> und Z<sub>4</sub> je eine Würfelfläche enthalten. | + | die Ebenen Z<sub>1</sub> und Z<sub>4</sub> je eine Würfelfläche enthalten. ''5 BE'' |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2005_V_2d_Lös.jpg|750px]] |
}} | }} | ||
| − | e) Der Eckpunkt G liegt in Z<sub>4</sub> (Nachweis nicht erforderlich). Berechnen Sie die Koordinaten von G. | + | e) Der Eckpunkt G liegt in Z<sub>4</sub> (Nachweis nicht erforderlich). Berechnen Sie die Koordinaten von G. ''4 BE'' |
:{{Lösung versteckt| | :{{Lösung versteckt| | ||
| − | [[Bild: | + | [[Bild:ABI_2005_V_2e_Lös.jpg|750px]] |
}} | }} | ||
Version vom 21. März 2010, 16:00 Uhr
|
|
|
a)Alle Scharebenen haben eine Gerade gemeinsam, die mit g bezeichnet wird. Geben Sie eine Gleichung von g an. 2 BE
c) Berechnen Sie, für welchen Wert des Parameters a die zugehörige Scharebene senkrecht auf der Scharebene Z1 steht. 4 BE
Der Punkt M(-1| 1 | 3) ist Mittelpunkt einer Kugel mit Radius
a)Zeigen Sie, dass der Punkt D auf dieser Kugel liegt, und berechnen Sie die Koordinaten des Kugelpunkts F, für den [FD] ein Durchmesser der Kugel ist. [Ergebnis: F(0 | 2 | 8)] 4 BE
|
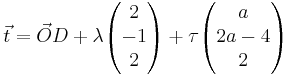 mit D (-2 | 0 | -2) und λ, τ, a є IR.
mit D (-2 | 0 | -2) und λ, τ, a є IR.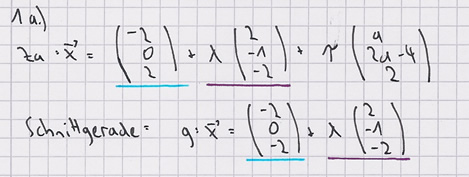
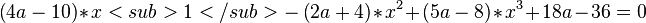 eine weitere mögliche Gleichung für die Ebenenschar Za ist.5 BE
eine weitere mögliche Gleichung für die Ebenenschar Za ist.5 BE
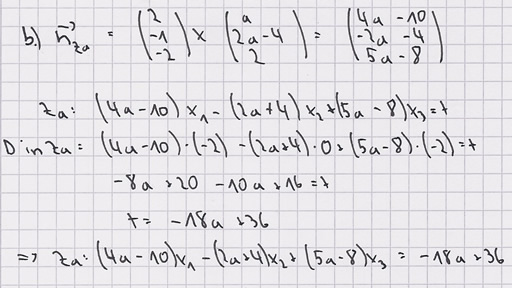


![\sqrt[3]{3}](/images/math/6/8/1/681d3d042b97f0fd1136ccaf260a53e5.png) .
.