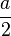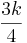Facharbeit Lernpfad Terme/Multiplizieren und Dividieren von Summen und Differenzen: Unterschied zwischen den Versionen
Aus RMG-Wiki
K (→Distributivgesetz der Multiplikation) |
K (→Distributivgesetz der Multiplikation) |
||
| Zeile 55: | Zeile 55: | ||
* (<math>\frac{1}{3}</math> -k)•<math>\frac{3}{4}</math> = <math>\frac{1}{3}</math> •<math>\frac{3}{4}</math> -k• <math>\frac{3}{4}</math> = <math>\frac{1}{4}</math> -<math>\frac{3k}{4}</math> | * (<math>\frac{1}{3}</math> -k)•<math>\frac{3}{4}</math> = <math>\frac{1}{3}</math> •<math>\frac{3}{4}</math> -k• <math>\frac{3}{4}</math> = <math>\frac{1}{4}</math> -<math>\frac{3k}{4}</math> | ||
</popup> </div> | </popup> </div> | ||
| + | <br /> | ||
| + | ==<span style="color: green">Distributivgesetz der Division </span> == | ||
Version vom 16. August 2010, 17:14 Uhr
Multiplizieren und Dividieren von Summen und Differenzen
Distributivgesetz der Multiplikation
|
Überlege nun, wie du das Produkt in eine Summe umwandeln kannst.
Erklärung:
Man multipliziert eine Summe (bzw. Differenz) mit einem Faktor, indem man jedes Glied der Summe (bzw. Differenz) mit dem Faktor multipliziert und die entstandenen Produkte addiert (bzw. subtrahiert).
- a•(b+c) = a•b+a•c = ab + ac für alle a, b, c

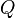
- a•(b-c) = a•b-a•c = ab - ac für alle a, b, c

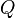
- (Vorgehensweise nach dem Distributivgesetz der Multiplikation)
Beispiel
(2-y)•3 = 2•3-y•3 = 6-3y
Multipliziere nun folgende Terme aus:
- (4+m)•2
- (7+z)•(-4)
- (
 +a)•
+a)•
- (
 -k)•
-k)•
 +
+