Benutzer:Neutert Jan-Peter: Unterschied zwischen den Versionen
(\Grenzwerte) |
(+symmetrie/+ableitung 1,2,3/+aufgaben) |
||
| Zeile 6: | Zeile 6: | ||
=== Welche Informationen kann ich aus einer Funktion bekommen? === | === Welche Informationen kann ich aus einer Funktion bekommen? === | ||
| − | • ''Wann berührt die Funktion die x - Achse? (genannt: Nullstelle)'' | + | • '''''<span style="color: darkorange">Wann berührt die Funktion die x - Achse? (genannt: Nullstelle)</span>''''' |
Dazu setzt man f(x) gleich Null und löst nach der Variablen x auf. Die Nullstelle hat die Koordinaten NS ( x / 0 ) | Dazu setzt man f(x) gleich Null und löst nach der Variablen x auf. Die Nullstelle hat die Koordinaten NS ( x / 0 ) | ||
| − | • ''Wann berührt die Funktion die y – Achse? (genannt: y – Achsenabschnitt)'' | + | • '''''<span style="color: darkorange">Wann berührt die Funktion die y – Achse? (genannt: y – Achsenabschnitt)</span>''''' |
| − | Um den y - Achsenabschnitt zu erhalten setzt man in die Funktion f(x) für x = 0 ein. Nach Auflösen des Terms erhält man den gewünschten y - Wert. Der y - Achsenabschnitt hat die Koordinaten AA ( 0 / y ) | + | Um den y - Achsenabschnitt zu erhalten setzt man in die Funktion f (x) für x = 0 ein. Nach Auflösen des Terms erhält man den gewünschten y - Wert. Der y - Achsenabschnitt hat die Koordinaten AA ( 0 / y ) |
| Zeile 26: | Zeile 26: | ||
| − | • ''Was passiert wenn die Funktion gegen ± ∞ geht?'' | + | • '''''<span style="color: darkorange">Was passiert wenn die Funktion gegen ± ∞ geht?</span>''''' |
Man lässt x gegen Unendlich laufen. Bei Polynomfunktionen klammert man immer die höchste Potenz aus, sodass man, aus den ganzen Summanden, ein Produkt erhält. Eine Beispielfunktion wäre: | Man lässt x gegen Unendlich laufen. Bei Polynomfunktionen klammert man immer die höchste Potenz aus, sodass man, aus den ganzen Summanden, ein Produkt erhält. Eine Beispielfunktion wäre: | ||
| − | f(x) = x³ - 2x² + x + 2 | + | f (x) = x³ - 2x² + x + 2 |
<math>\lim_{x\to\infty}</math>f (x) = <math>\lim_{x\to\infty}</math> x³ - <math>\frac{2}{x}</math> + <math>\frac{1}{x^2}</math> + <math>\frac{2}{x^3}</math> = <math>\lim_{x\to\infty}</math> x³ (1 - <math>\frac{2}{x}</math> + <math>\frac{1}{x^2}</math> + <math>\frac{2}{x^3}</math>) | <math>\lim_{x\to\infty}</math>f (x) = <math>\lim_{x\to\infty}</math> x³ - <math>\frac{2}{x}</math> + <math>\frac{1}{x^2}</math> + <math>\frac{2}{x^3}</math> = <math>\lim_{x\to\infty}</math> x³ (1 - <math>\frac{2}{x}</math> + <math>\frac{1}{x^2}</math> + <math>\frac{2}{x^3}</math>) | ||
| Zeile 35: | Zeile 35: | ||
Nun kann man einfach ablesen, dass <math>\lim_{x\to\infty}</math> x³ gegen <math>\infty</math> geht und die Klammer gegen 1, da alle Summanden die x im Nenner haben, gegen Null gehen. Daraus folgt das der Graph für + <math>\infty</math> gegen + <math>\infty</math> geht und für - <math>\infty</math> gegen - <math>\infty</math> geht. | Nun kann man einfach ablesen, dass <math>\lim_{x\to\infty}</math> x³ gegen <math>\infty</math> geht und die Klammer gegen 1, da alle Summanden die x im Nenner haben, gegen Null gehen. Daraus folgt das der Graph für + <math>\infty</math> gegen + <math>\infty</math> geht und für - <math>\infty</math> gegen - <math>\infty</math> geht. | ||
| + | |||
| + | |||
| + | • '''''<span style="color: darkorange">Ist die Funktion f (x) symmetrisch?</span>''''' | ||
| + | |||
| + | Es gibt zwei Arten von Symmetrien. Zum Einen die Achsensymmetrie, bei der die „linke Seite“ genauso aussieht wie die „rechte Seite“. Zum Anderen die Punktsymmetrie, bei der die „linke Seite“ auf die „rechte Seite“ abgebildet werden kann. | ||
| + | |||
| + | f (x + h) = f (x - h) <math>\Rightarrow</math> achsensymmetrisch zu einer Parallelen der y – Achse durch den Punkt ( x / f (x) ) | ||
| + | |||
| + | f (x + h) + f (x - h) = 2 f (x) <math>\Rightarrow</math> punktsymmetrisch zum Punkt ( x / f (x) ) | ||
| + | |||
| + | • '''''<span style="color: darkorange">Was bringen mir die Ableitungen von einer Funktion?</span>''''' | ||
| + | |||
| + | :''Wie leite ich eine Funktion ab?'' | ||
| + | |||
| + | {|width=90%| style="background-color:#F5F5F5; border: 1px solid #63B8FF; padding:0.5em" | ||
| + | | valign="top" | | ||
| + | Die allgemeine Ableitungsregel ist: '''<math>f (x) = x^n \Rightarrow f'(x) = n * x</math><sup>n-1</sup>''' | ||
| + | |} | ||
| + | |||
| + | |||
| + | '''Erste Ableitung''' | ||
| + | |||
| + | f ’(x<sub>1</sub>) = Steigung des Graphen im Punkt ( x<sub>1</sub> / f (x<sub>1</sub>) ) | ||
| + | |||
| + | f ’(x) = 0 <math>\Rightarrow</math> Man erhält die x – Werte, an denen sich Extrempunkte befinden. Um die genauen Koordinaten zu erhalten, setzt man den x – Wert in die Funktion f (x)ein. | ||
| + | |||
| + | |||
| + | '''Zweite Ableitung''' | ||
| + | |||
| + | f ’’(x<sub>1</sub>) > 0 <math>\rightarrow</math> Funktion f (x) ist an x<sub>1</sub> linksgekrümmt <math>\Rightarrow</math> ( x1 / f (x1) ) ist ein Minimum ! | ||
| + | |||
| + | f ’’(x<sub>1</sub>) < 0 <math>\rightarrow</math> Funktion f (x) ist an x<sub>1</sub> rechtsgekrümmt <math>\Rightarrow</math> ( x<sub>1</sub> / f (x<sub>1</sub>) ) ist ein Maximum ! | ||
| + | |||
| + | f ’’(x<sub>1</sub>) = 0 <math>\rightarrow</math> Funktion f (x) hat an der Stelle ( x<sub>3</sub> / f (x<sub>3</sub>) ) einen Terrassenpunkt ! | ||
| + | |||
| + | f ’’(x) = 0 <math>\rightarrow</math> Funktion f (x) hat an der Stelle ( x<sub>w</sub> / f (x<sub>w</sub>) ) einen möglichen Wendepunkt ! | ||
| + | |||
| + | |||
| + | {|width=90%| style="background-color:#F5F5F5; border: 1px solid #63B8FF; padding:0.5em" | ||
| + | | valign="top" | | ||
| + | Dies kann auch mit Hilfe der h-Methode überprüft werden. | ||
| + | |||
| + | Dazu schaut man sich <math>\lim_{h\to0} f' (x + h)</math> und <math>\lim_{h\to0} f' (x - h)</math> an. | ||
| + | |||
| + | Sind die Grenzwerte | ||
| + | :identisch, dann ist an der Stelle x<sub>1</sub> ein Terrassenpunkt. (Es gibt also keinen VZW der Steigung) | ||
| + | :nur vom Betrag gleich, dann ist an der Stelle x<sub>1</sub> ein Extrempunkt(Die Steigung hat an der Stelle einen VZW) | ||
| + | |||
| + | |} | ||
| + | |||
| + | '''Dritte Ableitung''' | ||
| + | |||
| + | f ’’’(x<sub>w</sub>) ≠ 0 <math>\rightarrow</math> Funktion f (x) hat an der Stelle ( x<sub>w</sub> / f (x<sub>w</sub>) ) '''einen''' Wendepunkt ! | ||
| + | |||
| + | f ’’’(x<sub>w</sub>) = 0 Funktion f (x) hat an der Stelle ( x<sub>w</sub> / f(x<sub>w</sub>) ) '''keinen''' Wendepunkt ! | ||
| + | |||
| + | |||
| + | ::<span style="color: darkblue">'''Bestimme von den folgenden Funktionen die Extremwertkoordinaten, entscheide ob es ein Maximum oder Minimum ist und errechne wenn möglich die Koordinaten des Wendepunktes.'''</span> | ||
| + | |||
| + | ::<span style="color: darkblue">'''Aufgabe 1: f (x) = x² + 2x - 6''' | ||
| + | |||
| + | ::{{Lösung versteckt|1= | ||
| + | ::Extrempunkt E( -1 / -7 ) | ||
| + | |||
| + | ::E ist ein Minimum! | ||
| + | |||
| + | ::Es gibt keinen Wendepunkt! | ||
| + | }} | ||
| + | |||
| + | |||
| + | ::<span style="color: darkblue">'''Aufgabe 2: f (x) = 6x³ - 6x² + 12x + 5''' | ||
| + | |||
| + | ::{{Lösung versteckt|1= | ||
| + | ::Es gibt keine Extremwerte! | ||
| + | |||
| + | ::Wendepunkt ( <math>\frac{1}{2}</math> / <math>\frac{1}{4}</math> ) | ||
| + | }} | ||
| + | |||
| + | |||
| + | ::<span style="color: darkblue">'''Aufgabe 3: f (x) = 2x<sup>4</sup> + 2 x² + 5''' | ||
| + | |||
| + | ::{{Lösung versteckt|1= | ||
| + | ::Extrempunkt E( 0 / 5 ) | ||
| + | |||
| + | ::E ist ein Minimum | ||
| + | |||
| + | ::Es gibt keinen Wendepunkt | ||
| + | }} | ||
| + | |||
| + | {|width=90%| style="background-color:#F5F5F5; border: 1px solid #63B8FF; padding:0.5em" | ||
| + | | valign="top" | | ||
| + | '''Bei Funktionen mit großen Exponenten wie zum Beispiel b (x) = x10 + 2x9 – 3x8 können natürlich auch von der dritten Ableitung, Extrema, Steigungen und Wendepunkte angeben. Dazu muss die dritte Ableitung der Funktion b (x) einfach wieder abgeleitet werden.''' | ||
| + | |} | ||
Version vom 29. Dezember 2009, 20:32 Uhr
Zum Einstieg: "Was ist und was bringt mir eine Funktion?"
Was ist eine Funktion?
So wie im täglichen Leben Statistiken oder Tabellen erstellt werden, können auch in der Mathematik sogenannte Funktionen erstellt werden. Diese sind, ähnlich wie bei einer Tabelle, abhängig von zwei meist unterschiedlichen Größen. Bei den mathematischen Funktionen ist es so, dass einer bestimmten Menge auf der x – Achse, eine bestimmte Menge auf der y - Achse zugeordnet wird. Bei rein mathematischen Überlegungen handelt es sich bei den beiden Mengen um den sogenannten x – Wert beziehungsweise y – Wert. Bei Funktionen mit Einheiten, wie zum Beispiel in der Physik der „Waagrechte Wurf“, wird dem x – Wert die Einheit Länge in Meter gegeben und dem y – Wert Höhe in Meter zugeteilt. Jedoch ist zu beachten, dass bei Funktionen jedem x - Wert nur ein y – Wert zugeordnet werden kann. Es ist also nicht möglich, dass eine Funktion mit dem x – Wert x1 zwei y – Werte y1 und y2 hat. Der Unterschied zwischen einer Funktion und einer Wertetabelle ist lediglich, dass die Funktion eine graphische Abbildung der Wertetabelle darstellt.
Welche Informationen kann ich aus einer Funktion bekommen?
• Wann berührt die Funktion die x - Achse? (genannt: Nullstelle)
Dazu setzt man f(x) gleich Null und löst nach der Variablen x auf. Die Nullstelle hat die Koordinaten NS ( x / 0 )
• Wann berührt die Funktion die y – Achse? (genannt: y – Achsenabschnitt)
Um den y - Achsenabschnitt zu erhalten setzt man in die Funktion f (x) für x = 0 ein. Nach Auflösen des Terms erhält man den gewünschten y - Wert. Der y - Achsenabschnitt hat die Koordinaten AA ( 0 / y )
- Wann besitzt der Graph einen y - Achsenabschnitt und eine Nullstelle?
- Nutze den Schieberegler um die Funktion zu verändern...
- !GeogebraApplet zu Nullstelle und Achsenabschnitt!
• Was passiert wenn die Funktion gegen ± ∞ geht?
Man lässt x gegen Unendlich laufen. Bei Polynomfunktionen klammert man immer die höchste Potenz aus, sodass man, aus den ganzen Summanden, ein Produkt erhält. Eine Beispielfunktion wäre: f (x) = x³ - 2x² + x + 2
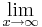 f (x) =
f (x) = 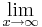 x³ -
x³ -  +
+ 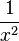 +
+ 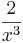 =
= 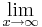 x³ (1 -
x³ (1 -  +
+ 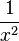 +
+ 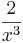 )
)
Nun kann man einfach ablesen, dass 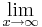 x³ gegen
x³ gegen  geht und die Klammer gegen 1, da alle Summanden die x im Nenner haben, gegen Null gehen. Daraus folgt das der Graph für +
geht und die Klammer gegen 1, da alle Summanden die x im Nenner haben, gegen Null gehen. Daraus folgt das der Graph für +  gegen +
gegen +  geht und für -
geht und für -  gegen -
gegen -  geht.
geht.
• Ist die Funktion f (x) symmetrisch?
Es gibt zwei Arten von Symmetrien. Zum Einen die Achsensymmetrie, bei der die „linke Seite“ genauso aussieht wie die „rechte Seite“. Zum Anderen die Punktsymmetrie, bei der die „linke Seite“ auf die „rechte Seite“ abgebildet werden kann.
f (x + h) = f (x - h)  achsensymmetrisch zu einer Parallelen der y – Achse durch den Punkt ( x / f (x) )
achsensymmetrisch zu einer Parallelen der y – Achse durch den Punkt ( x / f (x) )
f (x + h) + f (x - h) = 2 f (x)  punktsymmetrisch zum Punkt ( x / f (x) )
punktsymmetrisch zum Punkt ( x / f (x) )
• Was bringen mir die Ableitungen von einer Funktion?
- Wie leite ich eine Funktion ab?
|
Die allgemeine Ableitungsregel ist: |
Erste Ableitung
f ’(x1) = Steigung des Graphen im Punkt ( x1 / f (x1) )
f ’(x) = 0  Man erhält die x – Werte, an denen sich Extrempunkte befinden. Um die genauen Koordinaten zu erhalten, setzt man den x – Wert in die Funktion f (x)ein.
Man erhält die x – Werte, an denen sich Extrempunkte befinden. Um die genauen Koordinaten zu erhalten, setzt man den x – Wert in die Funktion f (x)ein.
Zweite Ableitung
f ’’(x1) > 0  Funktion f (x) ist an x1 linksgekrümmt
Funktion f (x) ist an x1 linksgekrümmt  ( x1 / f (x1) ) ist ein Minimum !
( x1 / f (x1) ) ist ein Minimum !
f ’’(x1) < 0  Funktion f (x) ist an x1 rechtsgekrümmt
Funktion f (x) ist an x1 rechtsgekrümmt  ( x1 / f (x1) ) ist ein Maximum !
( x1 / f (x1) ) ist ein Maximum !
f ’’(x1) = 0  Funktion f (x) hat an der Stelle ( x3 / f (x3) ) einen Terrassenpunkt !
Funktion f (x) hat an der Stelle ( x3 / f (x3) ) einen Terrassenpunkt !
f ’’(x) = 0  Funktion f (x) hat an der Stelle ( xw / f (xw) ) einen möglichen Wendepunkt !
Funktion f (x) hat an der Stelle ( xw / f (xw) ) einen möglichen Wendepunkt !
|
Dies kann auch mit Hilfe der h-Methode überprüft werden. Dazu schaut man sich Sind die Grenzwerte
|
Dritte Ableitung
f ’’’(xw) ≠ 0  Funktion f (x) hat an der Stelle ( xw / f (xw) ) einen Wendepunkt !
Funktion f (x) hat an der Stelle ( xw / f (xw) ) einen Wendepunkt !
f ’’’(xw) = 0 Funktion f (x) hat an der Stelle ( xw / f(xw) ) keinen Wendepunkt !
- Bestimme von den folgenden Funktionen die Extremwertkoordinaten, entscheide ob es ein Maximum oder Minimum ist und errechne wenn möglich die Koordinaten des Wendepunktes.
- Aufgabe 1: f (x) = x² + 2x - 6
- Extrempunkt E( -1 / -7 )
- E ist ein Minimum!
- Es gibt keinen Wendepunkt!
- Aufgabe 2: f (x) = 6x³ - 6x² + 12x + 5
- Es gibt keine Extremwerte!
- Wendepunkt (
 /
/  )
)
- Wendepunkt (
- Aufgabe 3: f (x) = 2x4 + 2 x² + 5
- Extrempunkt E( 0 / 5 )
- E ist ein Minimum
- Es gibt keinen Wendepunkt
|
Bei Funktionen mit großen Exponenten wie zum Beispiel b (x) = x10 + 2x9 – 3x8 können natürlich auch von der dritten Ableitung, Extrema, Steigungen und Wendepunkte angeben. Dazu muss die dritte Ableitung der Funktion b (x) einfach wieder abgeleitet werden. |
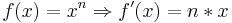 n-1
n-1
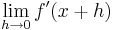 und
und 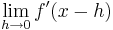 an.
an.

