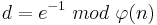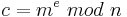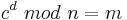RSA-Algorithmus
Nachfolgende Abkürzungen benötigst du für den RSA-Algorithmus:
| Abkürzung | Bedeutung |
|---|---|
| m (message) | Klartext |
| c (chiffre) | Chiffre |
| e (encryption) | Verschlüsselungsparameter |
| d (decryption) | Entschlüsselungsparameter |
Am 03.08. reist Bob mittags um 12 Uhr pünktlich mit dem Zug an. Alice hat ihre Recherchen bezüglich RSA erfolgreich abgeschlossen und erläutert Bob nun das RSA-Verfahren, das sie als geeignetes System ausgewählt hat.
Schlüsselerzeugung für das RSA-Public-Key-Kryptosystem:
Wie bereits besprochen, sollten sich Alice und Bob jeweils ein Schlüsselpaar generieren.
Dazu wählt man zwei, in etwa gleich große Primzahlen p und q, die jeweils eine Länge von ungefähr 512 - 2048 Bit haben. Anschließend bildet man durch Multiplikation von p und q den Modulus n.
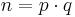
Nach dem Satz von Euler gilt also für 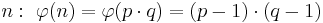
Nun wählt man sich eine natürliche Zahl e für die gilt:
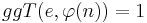 (Begründung folgt später beim Beweis des RSA-Kryptosystems)
(Begründung folgt später beim Beweis des RSA-Kryptosystems)
n und e bilden zusammen den öffentlichen Schlüssel.
Der private Schlüssel besteht aus d und n, d wird nun so bestimmt, dass gilt:
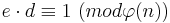
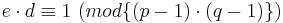
Folglich bildet d die modulo Inverse zu e und kann, wie in Algorithmus 2.4 beschrieben, bestimmt werden.
| Public-Key-RSA-Schlüsselerzeugung: | Public-Key-RSA-Ver- und Entschlüsselung: |
|---|---|
Algorithmus 3.0 (1) Alice erzeugt zwei große Primzahlen p und q von ungefähr der gleichen Länge, wobei die Länge der einzelnen Primzahlen zwischen 512 und 2048 Bit betragen sollte. |
Algorithmus3.1
Zusammenfassung: Bob chiffriert eine Nachricht m für Alice, die diese dechiffriert.
(2) Zur Dechiffrierung führt Alice den folgenden Schritt aus:
|
Bob kann sich nicht vorstellen, dass beim Entschlüsseln wirklich der Klartext wieder erscheint. Alice zeigt Bob den zugehörigen Satz und macht einen mathematischen Beweis, um Bob von der Korrektheit des Verfahrens zu überzeugen.
Satz 3.2 Es sei 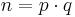 mit Primzahlen p und q, wobei
mit Primzahlen p und q, wobei 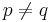 . Weiter gelte
. Weiter gelte 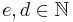 mit
mit 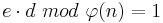 , und es sei
, und es sei ![m\in [0, n-1]](/images/math/7/0/7/7076a665adeb47067a38a1be448a3b03.png) eine Nachricht. Dann folgt.
eine Nachricht. Dann folgt.
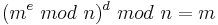 .
.
Beweis: 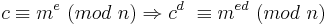
Wenn ggT (m,p) = 1, so gilt:
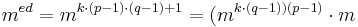
und daher nach dem Satz von Fermat 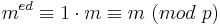
Ist m nicht zu p teilerfremd, so folgt 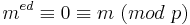 . Analog ergibt sich
. Analog ergibt sich 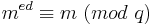 .
.
Insgesamt folgt, dass sowohl p als auch q und damit auch ihr Produkt 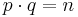 Teiler von
Teiler von
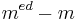 sind. Also gilt:
sind. Also gilt:
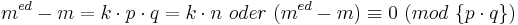
Damit gilt: 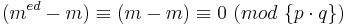
Nach den kennen gelernten Modul-Rechenregeln folgt also:
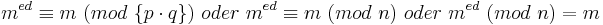 □
□
Nachdem sich Bob nach der „Modulo-Inverse“-Frage von Alice auch mit den mathematischen Grundlagen von RSA beschäftigt hat, erkennt er, dass Alice Recht hat und bei der Dechiffrierung tatsächlich wieder der Klartext erscheint.
Wer einen ausführlicheren Beweis wünscht, der findet diesen hier.
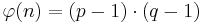 .
.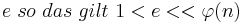 , mit
, mit