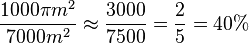BMT 10 2016
Aufgabe 1
| a) | Vereinfachen Sie so weit wie möglich.
|
| b) | Untersuchungen haben ergeben, dass ein durchschnittlicher Vier-Personen-Haushalt etwa 500 Euro pro Jahr einsparen könnte, wenn keine unverdorbenen Lebensmittel weggeworfen werden würden. Bestimmen Sie auf der Grundlage dieser Untersuchungen den Geldbetrag, der in Deutschland (80 Millionen Einwohner) jährlich eingespart werden könnte. |
- 80 Millionen Einwohnern können 20 Millionen Vier-Personen-Haushalte bilden.
- 20 Millionen · 500 Euro = 10 000 Millionen Euro = 10 Milliarden Euro
| c) | Hannah und Marie lesen in der Zeitung: „Fast 40 % der in den USA verkauften Lebensmittel landen im Müll“.
Marie sagt: „Die USA haben ungefähr 300 Millionen Einwohner, dann könnte man mit den weggeworfenen Lebensmitteln ungefähr 40 % von 300 Millionen, also 120 Millionen Menschen ernähren.“ Ergänzen Sie sinnvoll, was Hannah dazu sagen könnte. „Du irrst. Wenn 40 % der verkauften Lebensmittel im Müll landen, dann reichen ____% der verkauften Lebensmittel aus, um 300 Millionen Menschen zu ernähren. Mit den weggeworfenen Lebensmitteln könnte man ______ Millionen Menschen ernähren, weil ...“ |
- … 60 % … 200 Millionen …, weil
- 60 % für 300 Millionen reichen, 20 % also für 100 Millionen und 40 % für 200 Millionen.
Aufgabe 2
Simon möchte seinen Gartenteich mit einer Brücke überspannen, deren Auflagepunkte 8m voneinander entfernt sind. Dazu fertigt er eine Graphik an, die den Brückenbogen vereinfacht darstellt.
Der Brückenbogen wird durch eine Funktionsgleichung der Form I, II oder III mit a IR\{0} beschrieben.
- I y = a·(x2 - 8) II y = a·x·(x - 4) III y = a·x·(x - 8)
| a) | Begründen Sie, dass weder eine Gleichung der Form I noch eine der Form II zur Beschreibung des Brückenbogens infrage kommt. |
- Eine Gleichung der Form I kommt nicht infrage, da sie zu einer Parabel mit dem Scheitel bei x = 0 gehört. Der Scheitel der abgebildeten Parabel liegt aber bei x = 4.
- Eine Gleichung der Form II kommt nicht infrage, da sie zu einer Parabel mit den Nullstellen x1 = 0 und x2 = 4 gehört. Die abgebildete Parabel hat keine Nullstelle bei x = 4.
| b) | Der Brückenbogen wird also durch eine Funktionsgleichung der Form III beschrieben.
Berechnen Sie mithilfe der Graphik den passenden Wert von a. |
- Koordinaten des Scheitelpunkts in die Gleichung einsetzen:
- 1 = a · 4 · (4 - 8)
- 1 = a · (-16)
- a = -
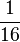
| c) | Mit der Gleichung der Form III und dem passenden Wert für a berechnet Simon den y-Wert für x = 6. Beschreiben Sie die Bedeutung dieses y-Werts im Sachzusammenhang. |
- Der y-Wert steht für die Höhe der Brücke in 6m Entfernung vom linken Auflagepunkt (bzw. in 2m Entfernung vom rechten Auflagepunkt).
Aufgabe 3
Ein Laplace-Würfel, der mit den Zahlen 1 bis 6 beschriftet ist, wird zweimal nacheinander geworfen. Bestimmen Sie die Wahrscheinlichkeit dafür, dass man die Augensumme 10 erhält.
- P("Die Augensumme ist 10") = P(46; 55; 64)=
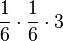 =
= 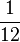
Aufgabe 4
Die Abbildung zeigt eine Pyramide der Höhe h. Die quadratische Grundfläche hat die Seitenlänge a, jedes Seitendreieck die Höhe m.
| a) | Ergänzen Sie die Gleichung
durch einen Term, mit dem h aus a und m berechnet werden kann. |
- m ist die Hypotenuse, h und
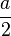 sind die Katheten eines rechtwinkligen Dreiecks. Es gilt der Satz des Pythagoras.
sind die Katheten eines rechtwinkligen Dreiecks. Es gilt der Satz des Pythagoras.
- Auflösen nach h ergibt:
Aufgabe 4b Mit welchen der folgenden Gleichungen lässt sich der Neigungswinkel ( |
Aufgabe 5
Auf einem Spielfeld, das 100 m lang und 75 m breit ist, findet ein Fußballspiel statt. Ein Spieler
passt den Ball zu einem Mitspieler; dabei ist der Ball zwei Sekunden unterwegs. Schätzen Sie den Anteil der Spielfeldfläche ab, den die zehn Feldspieler der gegnerischen Mannschaft in dieser Zeit höchstens abdecken können. Gehen Sie dazu davon aus, dass die Durchschnittsgeschwindigkeit der Spieler, während der Ball unterwegs ist, 5 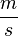 beträgt. Erläutern Sie Ihr Vorgehen.
beträgt. Erläutern Sie Ihr Vorgehen.
- Weg pro Spieler in 2 Sekunden: 5
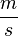 · 2s = 10m
· 2s = 10m
- höchstens abgedeckte Fläche pro Feldpieler (Kreis mit Radius 10m): (10m)2
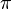 = 100
= 100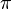 m2
m2
- von zehn Feldspielern höchstens abgedeckte Fläche: 1000
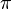 m2
m2
- Spielfeldfläche: 100m · 75m = 7500m2
- Anteil der Spielfeldfläche, die von zehn Feldspielern in 2 Sekunden höchstens abgedeckt werden kann:
Aufgabe 6
Bestimmen Sie die Lösung folgender Gleichung (Fehler beim Parsen(Syntaxfehler): x \in \mathbb{R} \backslash \lbrace{0;\frac{5}{4}\rbrace ).
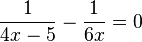
- 6x - (4x - 5) = 0
- 6x - 4x + 5 = 0
- 2x + 5 = 0
- x = -2,5
Aufgabe 7
| Im Dreieck ABC sind Ma , Mb und Mc die Mittelpunkte der Seiten (vgl. Abbildung). Die Verbindungsstrecken dieser Mittelpunkte mit den gegenüberliegenden Eckpunkten schneiden sich im Punkt S. |
| a) | Die Dreiecke AMcS und McBS haben den gleichen Flächeninhalt, da sie in der Länge einer Seite und der zugehörigen Höhe übereinstimmen. Tragen Sie diese Strecken deutlich sichtbar in die Abbildung ein. |
| b) | Analog zu Aufgabe 7a kann man zeigen, dass zwei weitere Paare von Dreiecken mit gemeinsamem Eckpunkt S jeweils den gleichen Flächeninhalt haben. Die übereinstimmenden Inhalte sind mit X, Y und Z bezeichnet (vgl. Abbildung).
Begründen Sie, dass die Aussagen 2Z + X = 2Y + X sowie 2Z + Y = 2X + Y wahr sind,und folgern Sie daraus, dass X = Y = Z gilt. |
- Die Dreiecke AMcC und McBC sind inhaltsgleich, da sie in der Länge einer Seite und der dazugehörigen Höhe übereinstimmen. Es gilt daher: 2Z + X = 2Y + X
- Die Dreiecke AMaC und ABMa sind inhaltsgleich, da sie in der Länge einer Seite und der dazugehörigen Höhe übereinstimmen. Es gilt daher: 2Z + Y = 2X + Y
- Aus 2Z + X = 2Y + X folgt Z = Y, aus 2Z + Y = 2X + Y folgt Z = X. Es gilt also: X = Y = Z.
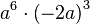
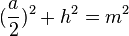
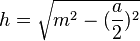
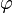 einer Seitenfläche gegen die Grundfläche berechnen? Kreuzen Sie an.
einer Seitenfläche gegen die Grundfläche berechnen? Kreuzen Sie an.
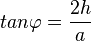 )
(!
)
(!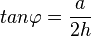 )
(!
)
(!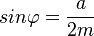 )
(
)
(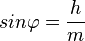 )
(!
)
(!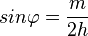 )
)