Abi 2013 Stochastik I Teil B: Unterschied zwischen den Versionen
| Zeile 22: | Zeile 22: | ||
;Aufgabe 1 | ;Aufgabe 1 | ||
| + | Folgende Tabelle gibt die Verteilung der Blutgruppen und der Rhesusfaktoren innerhalb der Bevölkerung Deutschlands wieder: | ||
| + | |||
[[Bild:ABI2013_SI_TeilB_1.jpg|center|350px]] | [[Bild:ABI2013_SI_TeilB_1.jpg|center|350px]] | ||
| − | a) | + | In einem Krankenhaus spenden an einem Vormittag 25 Personen Blut. Im Folgenden soll angenommen werden, dass diese 25 Personen eine zufällige Auswahl aus der Bevölkerung darstellen. |
| + | |||
| + | a)Bestimmen Sie die Wahrscheinlichkeit dafür, dass genau zehn der Spender die Blutgruppe A haben. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2013_SI_TeilB_1a_Lös.jpg|700px]] | [[Bild:ABI2013_SI_TeilB_1a_Lös.jpg|700px]] | ||
}} | }} | ||
| − | b) | + | b)Ermitteln Sie die Wahrscheinlichkeit dafür, dass mehr als die Hälfte der Spender die Blutgruppe 0 und den Rhesusfaktor Rh+ besitzt.<br /> |
| − | + | ||
| + | Folgende Tabelle gibt für die verschiedenen Empfänger von Spenderblut an, welches Spenderblut für sie jeweils geeignet ist: | ||
| + | [[Bild:ABI2013_SI_TeilB_1b.jpg|center|350px]] | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
| Zeile 37: | Zeile 43: | ||
}} | }} | ||
| − | c) | + | c) Für einen Patienten mit der Blutgruppe B und dem Rhesusfaktor Rh- wird Spenderblut benötigt. Bestimmen Sie, wie viele zufällig ausgewählte Personen mindestens Blut spenden müssten, damit man mit einer Wahrscheinlichkeit von mehr als 95 % mindestens eine für diesen Patienten geeignete Blutspende erhält. |
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2013_SI_TeilB_1c_Lös.jpg|700px]] | [[Bild:ABI2013_SI_TeilB_1c_Lös.jpg|700px]] | ||
| Zeile 52: | Zeile 59: | ||
;Aufgabe 2 | ;Aufgabe 2 | ||
| + | Bei 0,074 % der neugeborenen Kinder liegt eine bestimmte Stoffwechselstörung vor. Wird diese Störung frühzeitig erkannt, lässt sich durch eine geeignete Behandlung eine spätere Erkrankung vermeiden. Zur Früherkennung kann zunächst ein einfacher Test durchgeführt werden. Zeigt das Ergebnis des Tests die Stoffwechselstörung an, so bezeichnet man es als positiv. | ||
| + | Liegt bei einem neugeborenen Kind die Stoffwechselstörung vor, so ist das Testergebnis mit einer Wahrscheinlichkeit von 99,5 % positiv. Liegt bei einem neugeborenen Kind die Stoffwechselstörung nicht vor, so beträgt die Wahrscheinlichkeit dafür, dass das Testergebnis irrtümlich positiv ist, 0,78 %. | ||
| + | Bei einem zufällig ausgewählten neugeborenen Kind wird der Test durchgeführt. Betrachtet werden folgende Ereignisse: | ||
| + | :: S: „Die Stoffwechselstörung liegt vor.“ | ||
| + | :: T: „Das Testergebnis ist positiv.“<br /> | ||
a) | a) | ||
| + | Beschreiben Sie das Ereignis <math> \overline{S \cup T} </math> im Sachzusammenhang. | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2013_SI_TeilB_2a_Lös.jpg|700px]] | [[Bild:ABI2013_SI_TeilB_2a_Lös.jpg|700px]] | ||
| Zeile 59: | Zeile 72: | ||
b) | b) | ||
| + | Berechnen Sie die Wahrscheinlichkeiten P(T) und P<sub>T</sub>(S). Interpretieren Sie das Ergebnis für P<sub>T</sub>(S) im Sachzusammenhang. | ||
| + | :: (Zur Kontrolle: P(T) ≈ 0,85%, P<sub>T</sub>(S)<0,1) | ||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2013_SI_TeilB_2b_Lös.jpg|700px]] | [[Bild:ABI2013_SI_TeilB_2b_Lös.jpg|700px]] | ||
| Zeile 64: | Zeile 79: | ||
c) | c) | ||
| + | Im Rahmen eines Screenings wird eine sehr große Anzahl zufällig ausgewählter neugeborener Kinder getestet. Ermitteln Sie die pro Million getesteter Kinder im Mittel zu erwartende Anzahl derjenigen Kinder, bei denen die Stoffwechselstörung vorliegt und das Testergebnis negativ ist. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2013_SI_TeilB_2c_Lös.jpg|700px]] | [[Bild:ABI2013_SI_TeilB_2c_Lös.jpg|700px]] | ||
| Zeile 78: | Zeile 95: | ||
; Aufgabe 3 | ; Aufgabe 3 | ||
| − | a) | + | Um Geld für die Ausstattung des Spielbereichs in der Kinderstation des Krankenhauses einzunehmen, wird ein Gewinnspiel angeboten. Nachdem der Spieler zwei Euro bezahlt hat, werden aus einem Behälter, in dem sich drei rote, drei grüne und drei blaue Kugeln befinden, drei Kugeln ohne Zurücklegen zufällig entnommen. Haben die drei entnommenen Kugeln die gleiche Farbe, so gewinnt der Spieler und bekommt einen bestimmten Geldbetrag ausgezahlt; ansonsten verliert er und erhält keine Auszahlung. Anschließend werden die gezogenen Kugeln in den Behälter zurückgelegt.<br /> |
| + | |||
| + | a) | ||
| + | Zeigen Sie, dass bei einem Spiel die Wahrscheinlichkeit für einen Gewinn 1/28 beträgt. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2013_SI_TeilB_3a_Lös.jpg|700px]] | [[Bild:ABI2013_SI_TeilB_3a_Lös.jpg|700px]] | ||
| Zeile 84: | Zeile 105: | ||
b) | b) | ||
| + | Berechnen Sie, welcher Geldbetrag im Fall eines Gewinns ausgezahlt werden muss, damit im Mittel eine Einnahme von 1,25 Euro pro Spiel für die Ausstattung des Spielbereichs erwartet werden kann. | ||
| + | |||
:{{Lösung versteckt|1= | :{{Lösung versteckt|1= | ||
[[Bild:ABI2013_SI_TeilB_3b_Lös.jpg|700px]] | [[Bild:ABI2013_SI_TeilB_3b_Lös.jpg|700px]] | ||
Version vom 15. April 2018, 11:51 Uhr
|
|
Folgende Tabelle gibt die Verteilung der Blutgruppen und der Rhesusfaktoren innerhalb der Bevölkerung Deutschlands wieder: In einem Krankenhaus spenden an einem Vormittag 25 Personen Blut. Im Folgenden soll angenommen werden, dass diese 25 Personen eine zufällige Auswahl aus der Bevölkerung darstellen. a)Bestimmen Sie die Wahrscheinlichkeit dafür, dass genau zehn der Spender die Blutgruppe A haben. b)Ermitteln Sie die Wahrscheinlichkeit dafür, dass mehr als die Hälfte der Spender die Blutgruppe 0 und den Rhesusfaktor Rh+ besitzt. Folgende Tabelle gibt für die verschiedenen Empfänger von Spenderblut an, welches Spenderblut für sie jeweils geeignet ist: c) Für einen Patienten mit der Blutgruppe B und dem Rhesusfaktor Rh- wird Spenderblut benötigt. Bestimmen Sie, wie viele zufällig ausgewählte Personen mindestens Blut spenden müssten, damit man mit einer Wahrscheinlichkeit von mehr als 95 % mindestens eine für diesen Patienten geeignete Blutspende erhält. |
Bei 0,074 % der neugeborenen Kinder liegt eine bestimmte Stoffwechselstörung vor. Wird diese Störung frühzeitig erkannt, lässt sich durch eine geeignete Behandlung eine spätere Erkrankung vermeiden. Zur Früherkennung kann zunächst ein einfacher Test durchgeführt werden. Zeigt das Ergebnis des Tests die Stoffwechselstörung an, so bezeichnet man es als positiv. Liegt bei einem neugeborenen Kind die Stoffwechselstörung vor, so ist das Testergebnis mit einer Wahrscheinlichkeit von 99,5 % positiv. Liegt bei einem neugeborenen Kind die Stoffwechselstörung nicht vor, so beträgt die Wahrscheinlichkeit dafür, dass das Testergebnis irrtümlich positiv ist, 0,78 %. Bei einem zufällig ausgewählten neugeborenen Kind wird der Test durchgeführt. Betrachtet werden folgende Ereignisse:
a)
Beschreiben Sie das Ereignis b) Berechnen Sie die Wahrscheinlichkeiten P(T) und PT(S). Interpretieren Sie das Ergebnis für PT(S) im Sachzusammenhang.
c) Im Rahmen eines Screenings wird eine sehr große Anzahl zufällig ausgewählter neugeborener Kinder getestet. Ermitteln Sie die pro Million getesteter Kinder im Mittel zu erwartende Anzahl derjenigen Kinder, bei denen die Stoffwechselstörung vorliegt und das Testergebnis negativ ist. |
Um Geld für die Ausstattung des Spielbereichs in der Kinderstation des Krankenhauses einzunehmen, wird ein Gewinnspiel angeboten. Nachdem der Spieler zwei Euro bezahlt hat, werden aus einem Behälter, in dem sich drei rote, drei grüne und drei blaue Kugeln befinden, drei Kugeln ohne Zurücklegen zufällig entnommen. Haben die drei entnommenen Kugeln die gleiche Farbe, so gewinnt der Spieler und bekommt einen bestimmten Geldbetrag ausgezahlt; ansonsten verliert er und erhält keine Auszahlung. Anschließend werden die gezogenen Kugeln in den Behälter zurückgelegt. a) Zeigen Sie, dass bei einem Spiel die Wahrscheinlichkeit für einen Gewinn 1/28 beträgt. b) Berechnen Sie, welcher Geldbetrag im Fall eines Gewinns ausgezahlt werden muss, damit im Mittel eine Einnahme von 1,25 Euro pro Spiel für die Ausstattung des Spielbereichs erwartet werden kann.
|
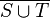 im Sachzusammenhang.
im Sachzusammenhang.

