Funktionenl

Teste dein Wissen

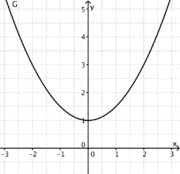
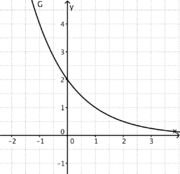
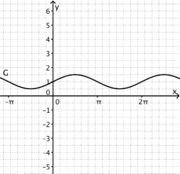
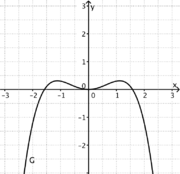
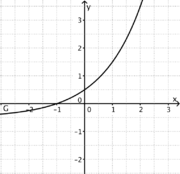
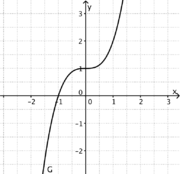
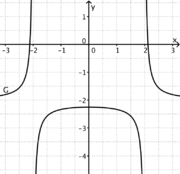
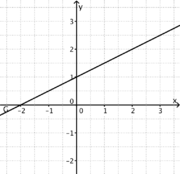
1) Ordne Funktionstyp, Funktionsterm und Funktionsgraph passend zu.

$f_5(x)=0,5x+1$

$f_4(x)=0,5x^2+1$

$f_6(x)=\frac {1}{x^2-4}-2$

$f_8(x)=2^x-0,5$

$f_7(x)=2\cdot (\frac 1 2)^x$

$f_2(x)=0,5sinx+1$

$f_1(x)=x^3+1$

$f_3(x)=-0,2x^4+0,5x^2$

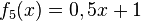
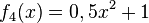
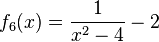
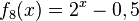
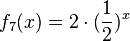
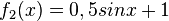
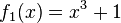
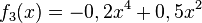
Trigonometrische FunktionGanzrationale FunktionExponentialfunktionQuadratische Funktion

Exponentialfunktion

Lineare FunktionGanzrationale FunktionGebrochen-rationale Funktion

Entscheide, ob P(3/-6) auf dem Graphen der Funktion 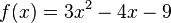$f(x)=3x^2-4x-9$ liegt.

1. Nein, P liegt unterhalb von G_f
2. Ja, P liegt auf G_f
3. Nein, P liegt oberhalb von G_f

prüfen!

3) Gib den Funktionsterm einer Geraden durch P(1/5) an, die parallel zur Geraden g: y=2x+4 verläuft.

Pluspunkt für eine richtige Antwort:
Minuspunkte für eine falsche Antwort:
Ignoriere den Fragen-Koeffizienten:

1.

p(x)=

Punkte: 0 / 0

4) Kreuze für 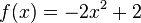$f(x)= -2x^2+2$ die richtige Aussage an: Versuche die Aufgabe durch Überlegen zu lösen; es sind keine Berechnungen nötig

1. G_f ist weiter als die Normalparabel
2. G_f ist achsensymmetrisch bzgl des y-Achse
3. G_f hat keinen Schnittpunkt mit der x-Achse
4. Der Grenzwert für x gegen minus unendlich ist unendlich
5. G_f ist nicht symmetrisch
6. Der Grenzwert für x gegen unendlich ist 0
7. G_f hat zwei Schnittpunkte mit der x-Achse
8. Der Grenzwert für x gegen unendlich ist unendlich
9. G_f hat einen Schnittpunkt mit der x-Achse
10. G_f ist enger als die Normalparabel
11. G_f hat die Form einer Normalparabel
12. G_f ist punktsymmetrisch bzgl des Ursprungs

Pluspunkt für eine richtige Antwort:    Syntaxfehler Minuspunkte für eine falsche Antwort: Ignoriere den Fragen-Koeffizienten: 1. Gib das Verhalten der folgenden Funktionen für $x \rightarrow \infty \, und \, x \rightarrow \infty$ an. Gib den Grenzwert als Dezimalzahl an oder verwende "u" für $\infty$ und "-u" für $-\infty$. $f(x)=\frac 1 x + \frac 3 5 \qquad \lim_{x \to \infty}f(x)=$ $f(x)=\frac 1 x + \frac 3 5 \qquad \lim_{x \to -\infty}f(x)=$ $f(x)=\frac {3x^4+2} {-5x^4+1} \qquad \lim_{x \to \infty}f(x)=$ $f(x)=\frac {3x^4+2} {-5x^4+1} \qquad \lim_{x \to -\infty}f(x)=$ $f(x)=\frac {3x^5+4x^2} {x^2-5x^4} \qquad \lim_{x \to \infty}f(x)=$ $f(x)=\frac {3x^5+4x^2} {x^2-5x^4} \qquad \lim_{x \to -\infty}f(x)=$ $f(x)=\frac {3x^2-x-3x^5} {5x^5+x+1} \qquad \lim_{x \to \infty}f(x)=$ $f(x)=\frac {3x^2-x-3x^5} {5x^5+x+1} \qquad \lim_{x \to -\infty}f(x)=$ $f(x)=\frac 3 5 x^3 \frac 3 5 x^2 \qquad \lim_{x \to \infty}f(x)=$ $f(x)=\frac 3 5 x^3 \frac 3 5 x^2 \qquad \lim_{x \to -\infty}f(x)=$ $f(x)=5 \cdot (\frac 1 3)^x \qquad \lim_{x \to \infty}f(x)=$ $f(x)=5 \cdot (\frac 1 3)^x \qquad \lim_{x \to -\infty}f(x)=$ Punkte: 0 / 0

prüfen!