Tonraumzahlen2
Aus RMG-Wiki
Beweis der Rechenregeln für den Logarithmus
Da dies nur Einzelbeispiele sind, sind die Rechenregeln nun zu beweisen (Aufbauend auf den Potenzgesetzen. Eine Einführung zu den Potenzgesetzen findet sich hier):
Der Logarithmus ist wie folgt definiert:
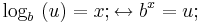
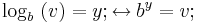
Für das Produkt folgt:
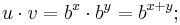
Wenn man wieder die Definition des Logarithmus anwendet erhält man:
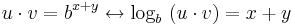
Wenn nun x und y durch die Werte von oben wieder ersetzt wird, bekommt man:
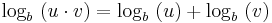
Analog folgt für den Quotienten 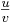 :
:
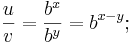
Anwendung der Definition des Logarithmus:
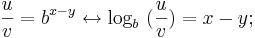
x und y ersetzen:
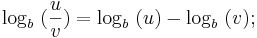
Das Vorziehen des Exponenten:
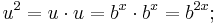
Anwendung der Definition des Logarithmus:
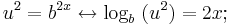
x ersetzen:
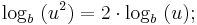
Analog ist
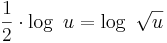
, da
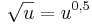 ist, also der letzte Beweis angewendet werden kann.
ist, also der letzte Beweis angewendet werden kann.
