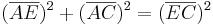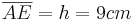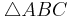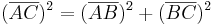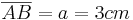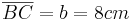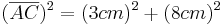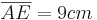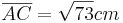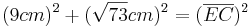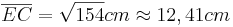Raumdiagonale

Berechnen der Raumdiagonalen in einem Quader

Du kennst sicher die Milchtüten aus dem Automaten an der Schule. Sie sind dreidimensional und haben eine Form, die sich Quader nennt.

Der Hersteller wollte nun wissen wie lang ein Strohhalm mindestens sein muss, damit man von einer Ecke diagonal zur unten liegenden kommt um die ganze Milch ohne Probleme trinken zu können.
Der Hersteller macht nur folgende Angaben:

Die Milchtüte ist:

• 8cm lang
• 3cm tief
• und 9cm hoch
  
  

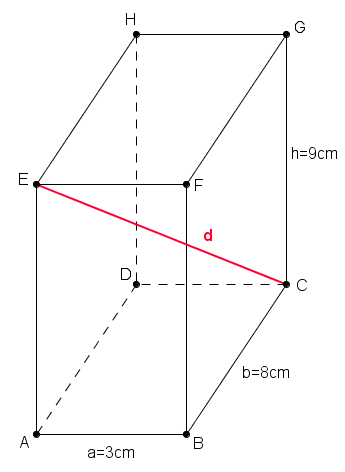
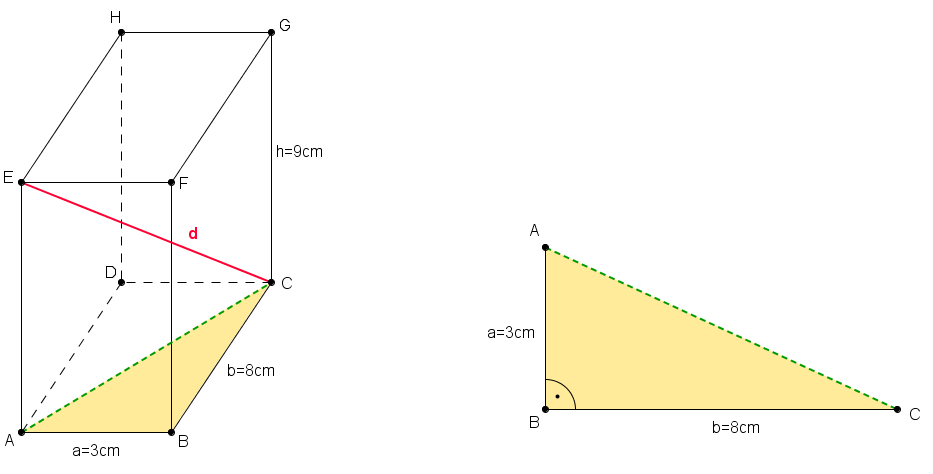
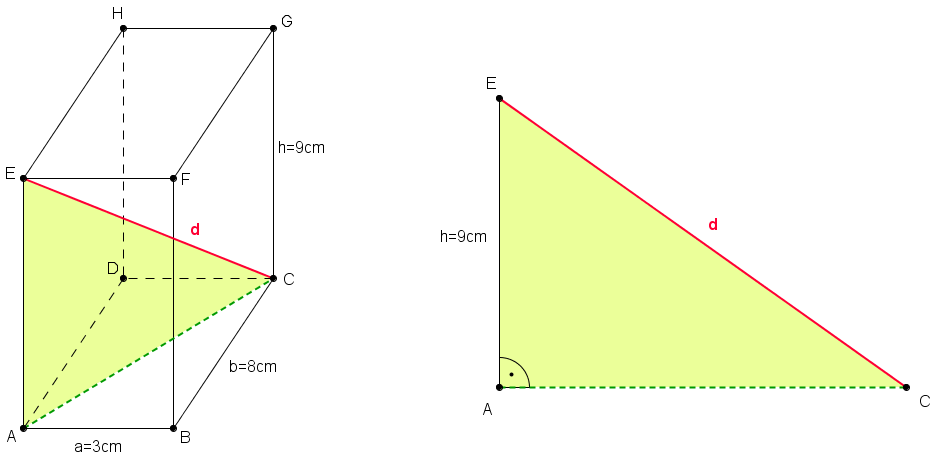
Zu diesem Problem siehst du hier eine Grafik. Die rote Strecke ${[EC]\,}$ soll der Strohhalm sein.

Zum vereinfachen der Rechnung geht man davon aus, dass der Strohhalm direkt durch die Ecke 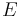${E\,}$ gestochen wird und bis zur Ecke 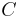${C\,}$ reichen soll.

Arbeitsauftrag:

• Zeichne den Quader in dein Heft!
• Überlege dir, wie man die Länge der Raumdiagonalen berechnen kann!

Arbeitsauftrag:

• Vergleiche deine Idee mit der Lösung

• Solltest du keine Idee haben, gehe die Schritte langsam druch, vielleicht fällt dir die Lösung doch noch auf

• Übertrage die Rechnung in dein Heft

[Lösung anzeigen][Lösung ausblenden]

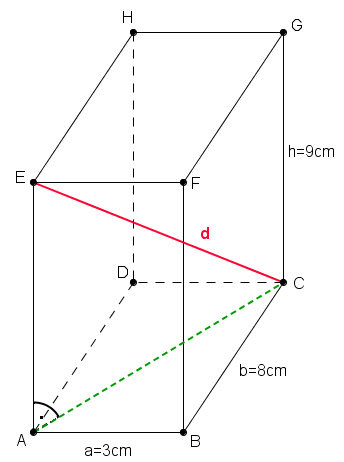
• Die Länge des Strohhalms ist eine Diagonale des Quaders

• Die Diagonale liegt im rechtwinkligen Dreieck $\triangle{ACE}$

[Lösung anzeigen][Lösung ausblenden]

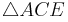
• Die Länge der Strecke ${[AC]\,}$ kann man mit Hilfe des Satzes des Pythagoras berechnen

• Die Länge beträgt:

• $(\overline{AE})^2 + (\overline{AC})^2 = (\overline{EC})^2$

• $\overline{AE}=h=9cm$

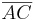• $\overline{AC}$ ist noch unbekannt und muss berechnet werden

[Lösung anzeigen][Lösung ausblenden]

• ${[AC]\,}$ liegt im rechtwinkligen Dreieck $\triangle{ABC}$

• $(\overline{AC})^2 = (\overline{AB})^2 + (\overline{BC})^2$

• $\overline{AB}=a=3cm$

• $\overline{BC}=b=8cm$

• Daraus folgt:

• $(\overline{AC})^2=(3cm)^2+(8cm)^2$

• $\overline{AC}=\sqrt{73}cm \approx 8,54cm$

[Lösung anzeigen][Lösung ausblenden]

• Es gilt:

• $(\overline{AE})^2 + (\overline{AC})^2 = (\overline{EC})^2$

• $\overline{AE}=9cm$

• $\overline{AC}=\sqrt{73}cm$

• $(9cm)^2 + (\sqrt{73}cm)^2 = (\overline{EC})^2$

• $\overline{EC}=\sqrt{154}cm \approx 12,41cm$

• Der Strohhalm müsste also mindestens 12,41cm lang sein